힙
우선순위 큐를 위해 고안된 완전이진트리의 일종이다.
힙의 특징
- 최댓값과 최솟값을 찾아내는 연산이 빠르다.
힙의 종류
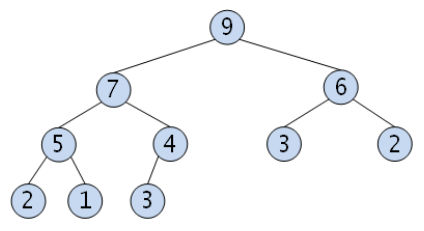
최대 힙(max heap)
부모 노드의 값이 자식 노드보다 크거나 같은 완전 이진 트리
=> 가장 큰 값이 루트 노드에 위치한다.
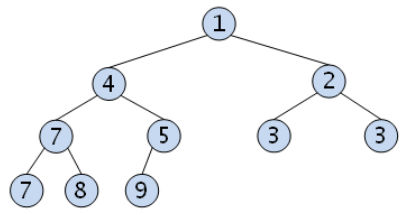
최소 힙(min heap)
부모 노드의 값이 자식 노드보다 작거나 같은 완전 이진 트리
=> 가장 작은 값이 루트 노드에 위치
힙 구현
- 힙 구현하는 표준적인 자료구조는 배열 이다.
- 구현의 편의성을 위해 배열의 첫 번째 인덱스를 0이 아닌 1로 사용한다.
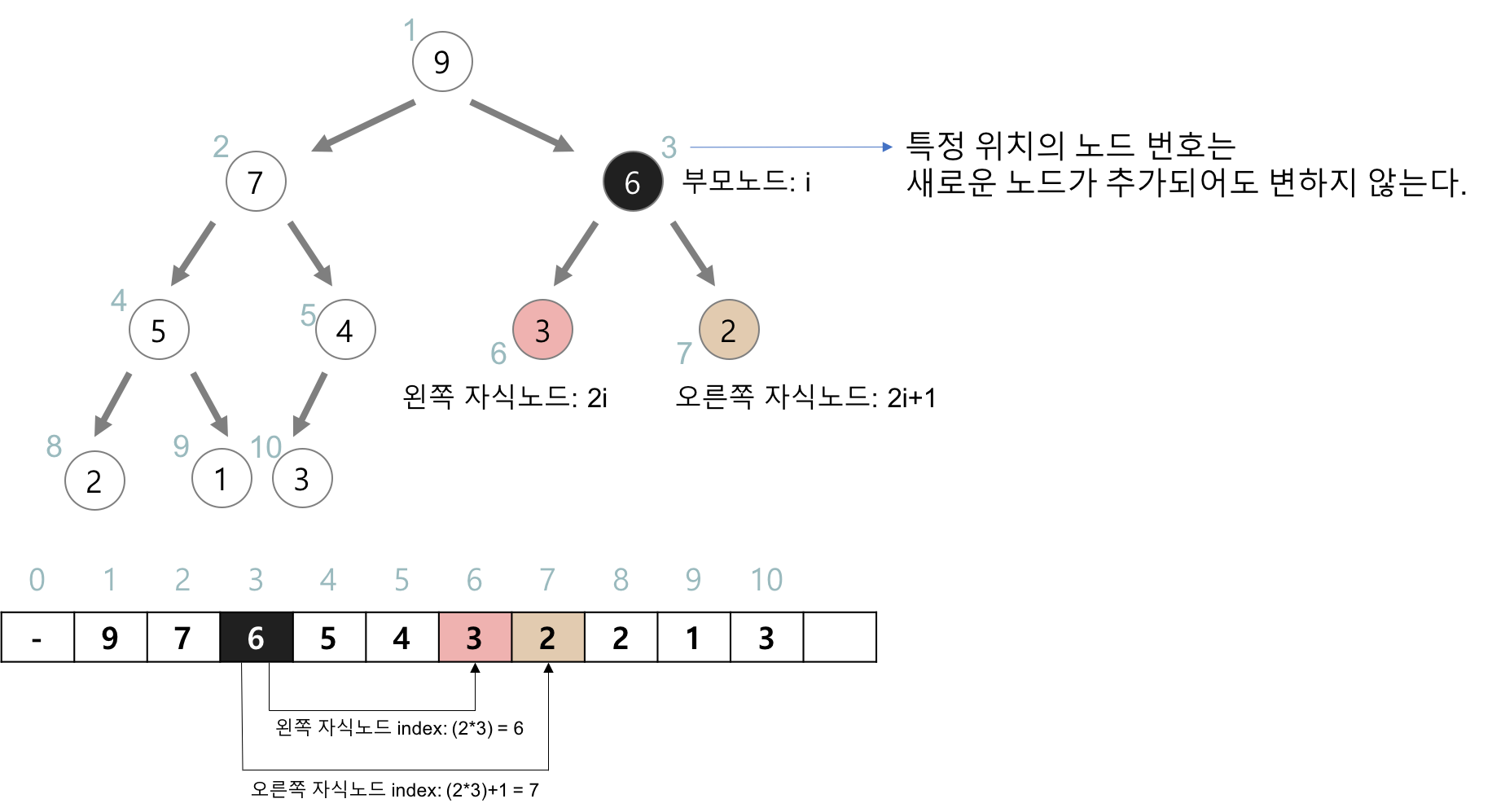
- 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다.
- 노드 위치가 곳 노드 번호가 된다. 즉, 자리가 번호
- 부모 노드와 자식 노드와의 관계
- left 자식 노드 index = (부모 index) * 2
- right 자식 노드 index = (부모 index) * 2
- index // 2 = 부모 index
힙 생성
- Heap 클래스를 생성해준다.
- 1번 인덱스부터 사용하기 위해 0번 자리에는 None을 삽입한다.
class Heap:
def __init__(self):
self.heap = []
self.heap.append(None)
힙의 삽입(heapify_up)
과정
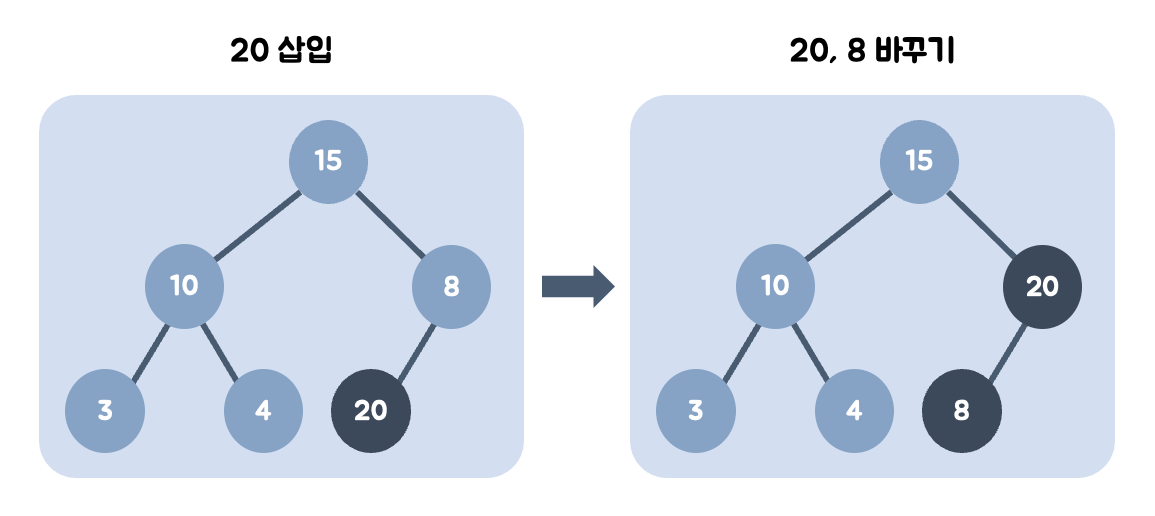
- 새로운 노드를 힙의 마지막 노드에 이어서 삽입
- 부모 노드들과 비교해서 위치 바꾸기
코드
def insert(self, data):
self.heap.append(data)
idx = len(self.heap) - 1
parent_idx = idx // 2
# heapify_up
# 부모 노드 보다 작아질 때까지 교환
while idx > 1 and self.heap[idx] > self.heap[parent_idx]:
self.heap[idx], self.heap[parent_idx] = (
self.heap[parent_idx],
self.heap[idx],
)
idx = parent_idx
힙의 삭제(heapify_down)
최대 힙의 경우 최대값을 최소 힙의 경우 최솟값을 삭제
루트 노드를 삭제 한 뒤에 힙을 재구성
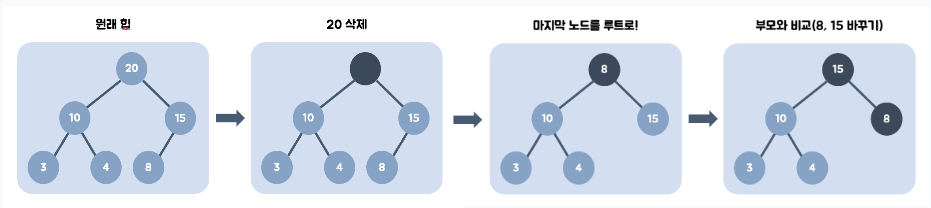
과정
- 루트 노드를 삭제
- 삭제된 루트 노드에 힙의 마지막 노드를 가져온다
- 힙을 재구성한다.
- 자식이 하나인 경우
- 자식이 둘인 경우
자식끼리 비교해서 더 큰 자식과 부모를 비교
-> 즉 루트노드에 올린다음에 노드를 끌어내릴 수 있을 때까지 끌어내린다.
코드
어떻게 두 자식 중에 더 큰 자식과 부모를 비교시킬 수 있을 지 고민했었는데 챗 GPT로 부터 힌트를 얻었다.
가장 큰 노드의 index만 가지고 있다가 왼쪽 오른쪽 모두 비교 후에 largest_index 와 부모 노드를 바꾸는 방법을 사용했다.
def pop(self):
if len(self.heap) == 1:
return None
if len(self.heap) == 2:
return self.heap.pop()
max_value = self.heap[1]
self.heap[1] = self.heap.pop()
# heapify_down
idx = 1
while idx * 2 < len(self.heap):
left_idx = idx * 2
right_idx = idx * 2 + 1
large_idx = idx
if self.heap[large_idx] < self.heap[left_idx]:
large_idx = left_idx
if (
right_idx < len(self.heap)
and self.heap[large_idx] < self.heap[right_idx]
):
large_idx = right_idx
if large_idx == idx:
break
if large_idx != idx:
self.heap[idx], self.heap[large_idx] = (
self.heap[large_idx],
self.heap[idx],
)
idx = large_idx
return max_value
파이썬에서 heaq 모듈 사용하기
파이썬에서는 heap도 모듈로 쉽게 사용할 수 있다.
python heapq 모듈