시간복잡도
어떤 문제를 해결하기 위한 코드가 있을 때, 해당 코드의 성능을 분석해서 과연 그 알고리즘이 효율적인 지 확인하는 과정이 필요하다.
성능을 분석하기 위한 방법
- 시간
- 연산 횟수
절대적인 시간을 기준으로하면 코드가 작동하는 환경에 많은 영향을 받는다.
→ 연산 횟수를 통해서 성능을 대략적으로 분석할 수 있다.
점근적 표기법
Big-O(빅오)
모든 n > n0에 대해 0 <= f(n) <= cg(n)인 양의 상수 c, n0가 존재하면 f(n) = O(g(n))
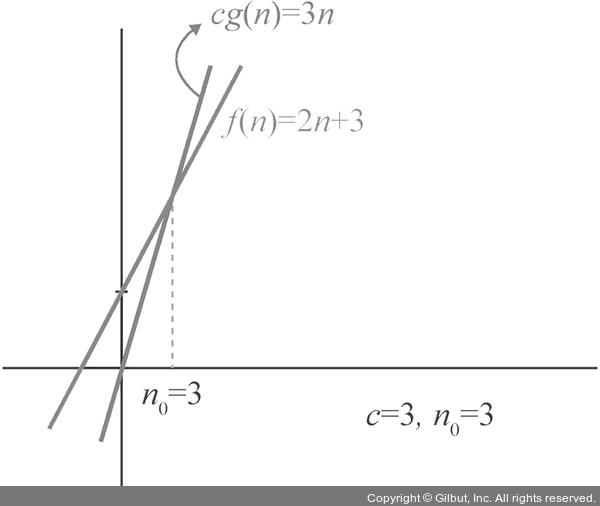
즉 n이 무한으로 갔을 때, 상한으로 접근하는 n의 최소 차수를 말합니다.
위에서는 2n+3은 O(n)을 가진다고 할 수 있다.
Big-Ω(빅-오메가
모든 n > n0에 대해 cg(n) <= f(n)인 양의 상수 c, n0가 존재하면 f(n) = Ω(g(n))
Big-θ(빅-세타)
모든 n > n0에 대해 c1g(n) <= f(n) <= c2g(n)인 양의 상수 c1, c2, n0가 존재하면 f(n) = θ(g(n))
Big-O 정리
O(1)
O(1)은 constant complexity라고 하여, 입력값이 증가하더라도 시간이 늘어나지 않는다.
상수의 시간 복잡도라는 의미이기 때문에, 입력값의 크기와 관계없이, 즉시 출력값을 얻어낼 수 있다.
예를 들면, 배열에 index로 직접접근하는 경우
O(log n)
O(log n)은 Logarithmic complexity라고 부르며 빅오 표기법 중 O(1) 다음으로 빠른 시간 복잡도를 가진다.
예로는 이진 탐색 트리 계열의 자료구조의 삽입과 탐색, 삭제 등.
O(n)
O(n)은 Linear complexity라 하며, 입력값이 증가함에 따라 시간 또한 선형적으로 증가한다.
대표적인 예로는 연결리스트의 탐색, 연산
O(nlong n)
O(n)과 비교했을 때는 성능이 나쁘지만 O(n2)과 비교하면 성능이 매우 좋다.
대표적인 예로 퀵 정렬과 병합 정렬
O(n^2)
입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가.
대표적인 예로 삽입, 선택, 버블 정렬등
O(2^n)
O(2n)은 기하급수적 복잡도(exponential complexity)라고 부르며, Big-O 표기법 중 가장 느린 시간 복잡도를 가진다.
function fibonacci(n) {
if (n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
코딩테스트를 위한 우리는 어떻게 시간복잡도를 활용할 수 있을까?
코딩 테스트는 결국 정해진 시간안에 주어진 문제들을 풀어내야 한다.
대부분의 알고리즘 문제들을 1~2초 정도의 시간제한을 둔다.
이 시간제한과 자신이 사용하는 언어의 계산 능력을 계산해서 어느 정도의 시간복잡도를 가지는 코드를 작성할 수 있는지 계산할 수 있고, 어느 알고리즘을 사용할 수 있는지 계산이 된다.
python은 1초에 2000만번의 연산, 그 외 언어들은 1초에 1억번의 연산으로 생각하면 된다.
예를 들어,
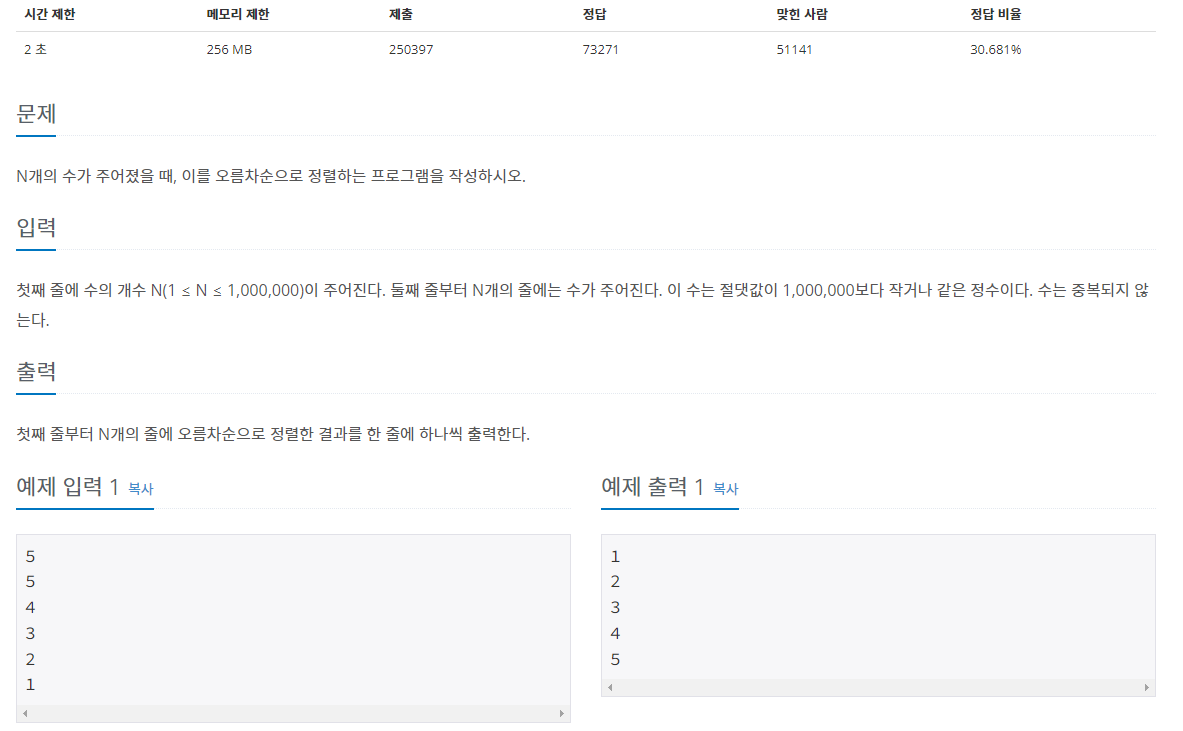
다음 같은 문제를 python으로 푼다고 했을 때,
- 제한 시간 2초 → 4000만번의 연산 가능.
- 입력값n 이 최대 1000000 → O(n^2) 은 불가능. O(nlogn) 가능.
이런식으로 O(nlogn) 의 알고리즘이 사용가능하다는 정보를 얻으면, O(n^2) 이상의 time complexity 를 가지는 알고리즘들은 제하고 그 이하의 알고리즘 안에서 생각을 해보면 된다는 것이다.