최단경로
최단 경로 알고리즘
말 그대로 가장 짧은 경로를 찾는 알고리즘을 의미한다.
- 문제를 그래프로 표현하고 각 지점을 노드, 지점간 연결된 도로를 간선이라고 한다
다익스트라 알고리즘 (Dijkstra Algorithm)
매번 가장 거리가 짧은 노드를 선택하고 거리 최신화
- 특정 노드에서 출발해서 모든 노드로 향하는 각각의 최단 경로를 구할 수 있다.
- 단, 가중치가 음인 값이 없어야 한다.
- 매번 가장 비용이 적은 노드를 선택하므로 그리디 알고리즘으로 분류된다
동작과정
- 출발 노드 설정
- 최단 거리 테이블 초기화(출발 노드=0, 나머지는 inf으로 설정)
- 방문하지 않은 노드 중에 가장 가까운 노드 선택
- 선택한 노드를 중심으로 거리 재계산
- 반복
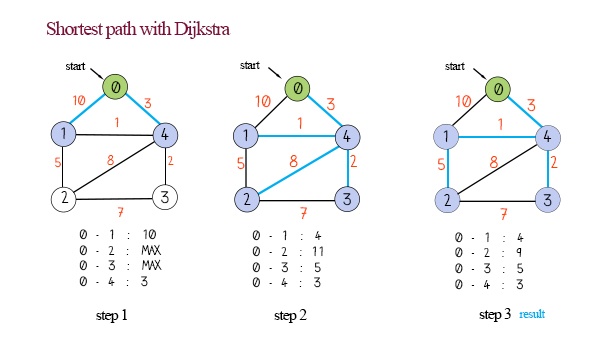
위 그림을 예로 들면
- 0 번 노드에서 출발.
- 가장 거리가 가까운 4 선택 ⇒ 거리 재계산
- 1,2,3중 가장 가까운 1번 노드 선택
- 2,3 중 가까운 3번 노드 선택
- 2번 노드 선택
각 선택마다 거리를 재계산한다.
구현
간선을 2차원 배열로 저장
INF=int(1e9)
distance = [INF for _ in range(v)]
visited = [False for _ in range(v)]
def min_distance_node():
min_distance = INF
min_idx = INF
for i in range(v):
if visited[i] == False and distance[i] < min_distance:
min_distance = distance[i]
min_idx = i
return min_idx
def dijkstra(start):
distance[start] = 0
next_node = start
while next_node < INF:
visited[next_node] = True
for i in range(v):
if graph[next_node][i] != INF and visited[i] == False:
distance[i] = min(
distance[i], distance[next_node] + graph[next_node][i]
)
next_node = min_distance_node()
이 경우 간선을 저장하기 위한 공간이 많이 생긴다.
간선을 리스트로 저장.
graph = [[] for _ in range(v + 1)]
distance = [INF] * (v + 1)
visited = [False] * (v + 1)
def min_distance_node():
min_distance = INF
min_idx = INF
for i in range(1, v + 1):
if visited[i] == False and distance[i] < min_distance:
min_distance = distance[i]
min_idx = i
return min_idx
def dijkstra(start):
distance[start] = 0
visited[start] = True
for i in graph[start]:
distance[i[0]] = i[1]
for _ in range(v - 1):
now = min_distance_node()
if now == INF:
break
visited[now] = True
for next in graph[now]:
distance[next[0]] = min(distance[now] + next[1], distance[next[0]])
dijkstra(k)
시간 복잡도
노드의 수를 V라고 할 때, v 개의 노드를 선택할 때마다 v번씩 거리 재계산이 필요하기 때문에 시간복잡도는 O(
다익스트라 알고리즘 : 개선된 방법
시작 노드와 거리가 가장 가까운 노드들을 선택해가는게 다익스트라다. 가장 가까운 노드를 선택하는데 우선순위 큐를 사용할 수 있다.
우선순위 큐를 사용하면 visited 배열이 없어도 된다.우선순위 큐가 최단 거리의 노드를 앞으로 정렬하므로 기존 최단 거리보다 크면 무시하면 되기 때문이다. 만약 기존 최단 거리보다 더 작은 값을 가지는 노드가 있다면 노드와 거리를 우선순위 큐에 넣는다
동작과정
- 모든 노드 거리 INF, 시작 노드는 0으로 초기화
- 우선 순위 큐에 시작 노드 삽입
- 우선순위 큐에서 min 노드 추출
- 해당 노드의 이웃 노드들 순회하며 거리 업데이트
- 업데이트 된 노드만 우선순위 큐에 삽입
- 우선순위 큐 빌 때 까지 3~5번 반복
코드
def dijkstra(start):
heap = []
heapq.heappush(heap, (0, start))
distance[start] = 0
while len(heap):
dis, node = heapq.heappop(heap)
# 현재 노드의 거리가 이미 처리한 거리보다 크면 스킵
# 거리가 중복 힙 삽입된 경우를 제외시키는 것.
if dis > distance[node]:
continue
# 인접 노드들 업데이트
for next_node, next_dis in graph[node]:
if distance[next_node] > dis + next_dis:
distance[next_node] = dis + next_dis
heapq.heappush(heap, (distance[next_node], next_node))
시간 복잡도
간선의 개수를 E, 노드의 개수를 V라고 할 때
각 노드를 방문할 때마다 간선으로 연결된 노드들의 길이를 업데이트한다. 이 연산은 V+E 번 반복되고, 이를 힙에 저장하므로 logV가 필요하다
=> 시간복잡도는 O((V+E)
Dijstra 순차탐색 vs 우선 순위 큐
- [!] 간선의 수가 노드 수에 비해 많을 경우 순차탐색이 더 빠를 수 있다.
참고 : 백준 1504번 - 특정한 최단 경로
벨만-포드 알고리즘 (Bellman-Ford-Moore Algorithm)
한 노드에서 다른 노드 까지의 최단 거리를 구하는 알고리즘
- 매 단계마다 모든 간선을 확인하면서 모든 노드간의 최단 거리를 구해나간다.
- 간선 가중치가 음수인 경우에도 사용할 수 있다.
- 시간 복잡도가 높기 때문에 음수가 아니라면 다익스트라 사용
동작과정
- 출발 노드 설정
- 최단 거리 테이블 초기화(출발 노드=0, 나머지는 inf으로 설정)
- 현재 노드의 모든 인접 노드 탐색해서 기존에 저장된 거리보다 짧을 경우 갱신
- 3의 과정을 모든 노드에 대해 수행
- 모든 노드에 대해 수행하고 또 거리가 갱신된다면 음의 무한대 발생시키는 음수 사이클 존재
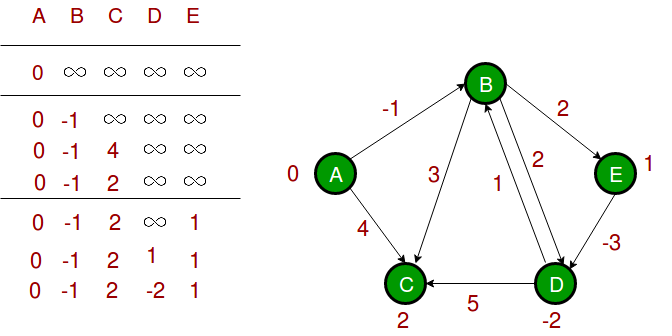
⇒ 쉽게 다익스트라의 모든 노드 버전이라고 생각하면 된다.
구현
edges = []
distance = [INF] * (v+1)
for _ in range(e):
a, b, c = map(int, input().split())
edges.append((a, b, c))
def bellman_ford(start):
distance[start] = 0
for i in range(v):
for j in range(e):
cur_node = edges[j][0]
next_node = edges[j][1]
edge_cost = edges[j][2]
if (
distance[cur_node] != INF
and distance[cur_node] + edge_cost < distance[next_node]
):
distance[next_node] = distance[cur_node] + edge_cost
# 음수 순환 체크
if i == v - 1:
return True
return False
- 모든 간선을 계속 반복해서 돌기 때문에 그래프를 굳이 가질 필요가 없다.
시간복잡도
노드 갯수 만큼 모든 간선을 탐색하므로 ==O(V*E)==의 시간 복잡도가 발생한다. 간선의 최대 갯수가 V^2가 될 수 있으므로 최악의 경우에 시간 복잡도는 ==O(V^3)==이 된다.
플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)
모든 지점에서 다른 모든 지점으로의 최단 경로를 구하는 알고리즘
- 소스코드가 짧아서 구현이 쉬움
- 2차원 테이블로 최단 거리 정보 저장.
- 음의 가선도 사용할 수 있다.
- 다익스트라는 그리디로 분류되는 반면, 플로이드는 DP로 분류될 수 있음
- 3중 반복으로 점화식에 따라서 최단 거리 테이블 갱신
- 시간 복잡도가 O(v^3)로 매우 크다.
플로이드-워셜 알고리즘 점화식
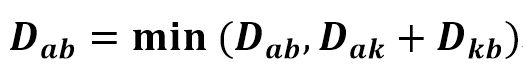
동작과정
- 2차원 최단 거리 테이블 초기화 → 자기 자신은 0, 간선 없으면 INF
- n번 노드를 경유하면서 점화식을 만족하는 값으로 최단 거리 테이블 갱신의 반복이다.

구현
for k in range(1, n + 1):
for a in range(1, n + 1):
for b in range(1, n + 1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
시간 복잡도
당연하게도 O(v^3)
reference
- https://www.lavivienpost.com/shortest-path-and-2nd-shortest-path-using-dijkstra-code/
- https://techblog-history-younghunjo1.tistory.com/247
- https://www.geeksforgeeks.org/bellman-ford-algorithm-dp-23/
- https://www.semanticscholar.org/paper/All-Pairs-Shortest-Paths-and-the-Floyd-Warshall-Mount/9cb9e82f482d434cf73ec2dd747662e0dc741caf