Union-Find

그래프 알고리즘인 최소신장트리#Kruskal MST 알고리즘 알고리즘과 위상정렬 알고리즘을 사용하기 위해서는 같은 그룹 내에 있는 정점인지 판별하는 작업이 필요하고 이를 위해 서로소 집합 알고리즘을 공부했다.

Disjoint Set

서로 중복되지 않는 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조 즉, 서로소 집합 자료구조

Union-Find 알고리즘

Disjoint Set을 구현할 때 사용하는 알고리즘

Find : 노드의 부모 노드를 찾는다.
Union : 집합으로 묶는다.

연산

Union-Find를 트리 구조로 구현하는 이유

  1. 배열
    배열로 집합 번호를 저장.
    • union(x,y)
      • 배열의 모든 원소를 순회하면서 y 집합 번호를 x 집합번호로 변경
      • 시간복잡도 : O(n)
    • find(x)
      • 한 번으로 x가 속한 집합 번호 찾을 수 있다.
      • 시간 복잡도 : O(1)
  2. 트리
    트리로 구현한 경우 union이 find 연산의 결과를 사용하기에 find 연산이 전체 연산이 된다.
    find 연산은 트리의 높이에 영향을 받는다.
    시간 복잡도 : O(logN)~O(N)

과정

  1. 모든 노드의 부모노드를 자신으로 초기화
  2. 두 노드의 각각의 부모 노드 Find
  3. 두 쌍 중 자식 노드의 부모노드를 Union
    이 과정에서 더 작은 값을 부모로 가정하기도 한다.
    https://techblog-history-younghunjo1.tistory.com/257
  4. 나머지 연산 정보로 순차적으로 2~3번 반복

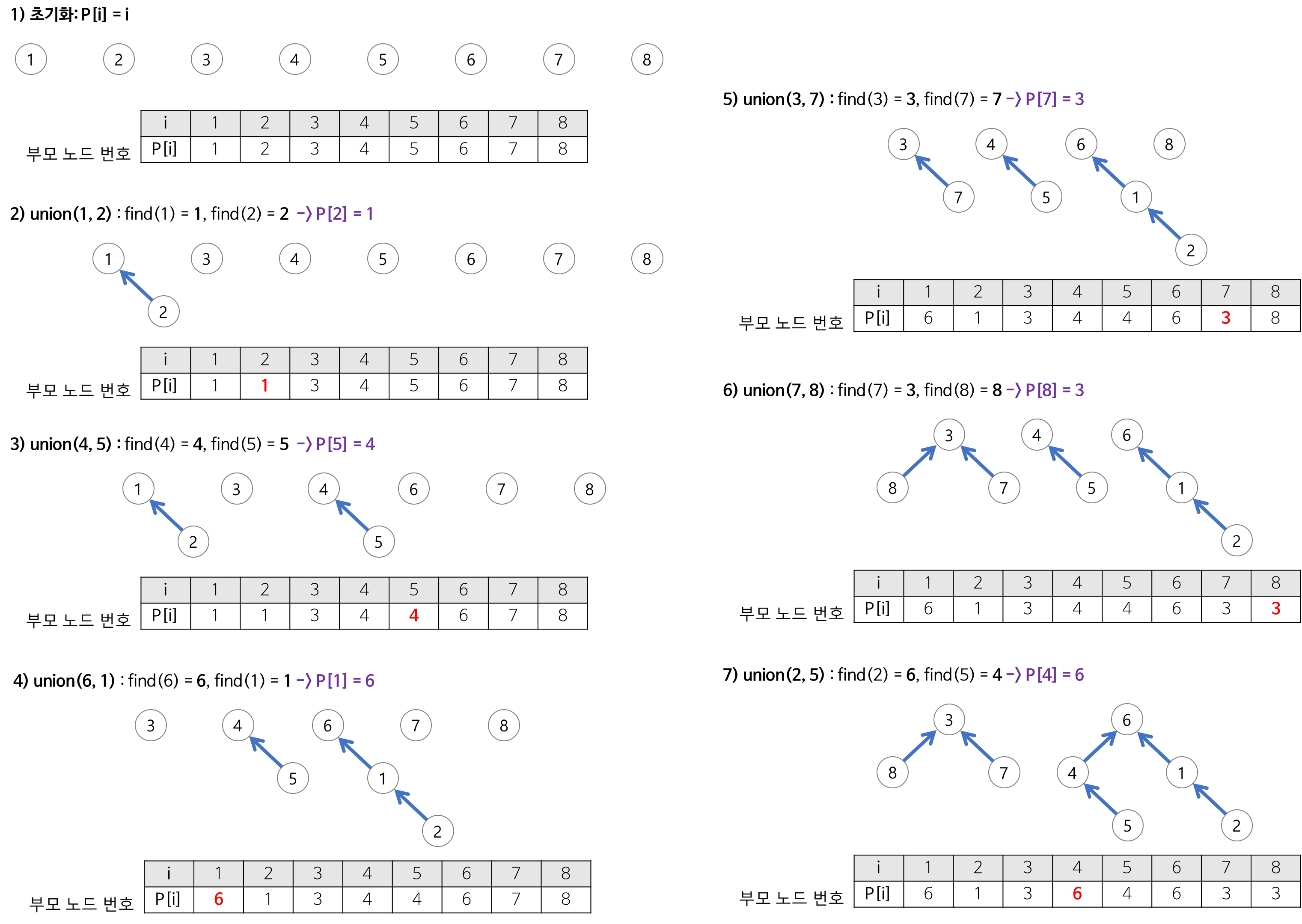
union-find-example.png

마지막 결과를 보면은 두 집합으로 나누어져 있다.
2번 노드의 경우 최종 루트 노드를 찾기 위해선 1번을 거쳐야 한다.
⇒ find 연산을 압축경로를 사용해서 최적화 할 수 있다.

구현

# 초기화
parent = [i for i in range(n + 1)]

# 부모 노드 찾기
def find(x):
    if x == parent[x]:
        return x
    return find(parent[x])
# 반목문으로
def find(x):
    while x != parent[x]:
        x = parent[x]
    return x

# 합치기
def union(x, y):
    parent[find(y)] = parent[find(x)]

시간 복잡도

일반적으로 트리의 높이만큼 탐색하므로 O(logN) 이지만, 트리가 편향되어 형성되는 최악의 경우 ==O(n)==의 시간복잡도를 가질 수 있다.

Union-Find 개선

최악의 상황

worst-case.png
트리의 구조가 비대칭인 경우 트리의 높이가 높아지고 find 연산의 시작복잡도가 O(n)으로 증가한다.

find 연산 최적화

path-compression.png
최악의 경우 linear treed에서 find 연산이 O(N) 의 시간복잡도를 가지므로 이를 해결해줘야 한다.
이를 해결하기 위해 2가지 방법을 사용한다.

  1. Union by rank
  2. path compression

Union by Rank

각 노드 별로 자신을 루트로 하는 subtree의 높이를 별도의 배열로 관리하여 union 과정에서 활용한다.

기존 union 과 어떻게 다르냐

subtree 높이가 낮은 쪽에 subtree 높이가 높은 쪽이 붙어서 트리 높이가 더 높아지는 것을 방지한다.
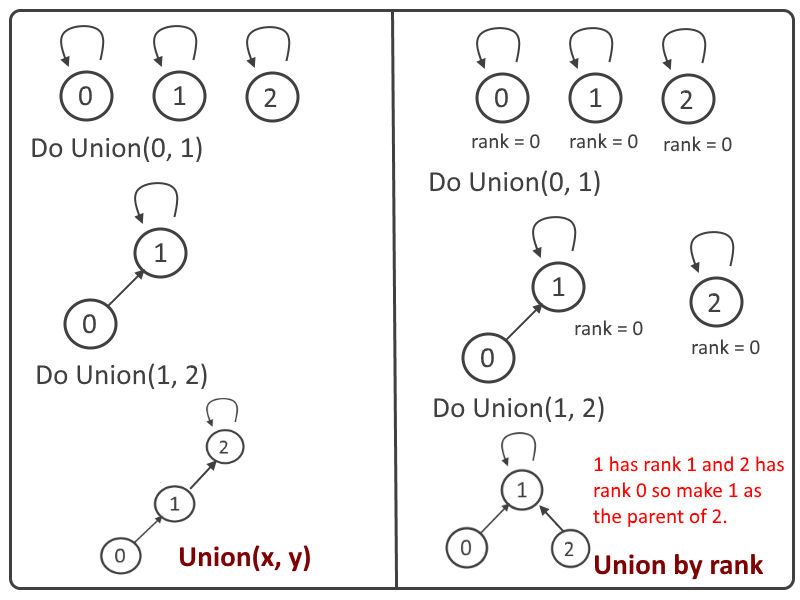
aa043b5331f67662baf74b74687d5ca6_MD5.jpg

과정
  1. 부모노드를 자신으로, rank를 0으로 배열 초기화
  2. union 과정에서 rank 비교
    • 두 랭크가 다르면
      큰 쪽으로 합치기
    • 두 랭크가 같으면
      임의로 한쪽의 rank +=1
코드
def find(x):
    while x != parent[x]:
        x = parent[x]
    return x

def union(x, y):
    a, b = find(x), find(y)
    if a != b:
        if rank[a] < rank[b]:
            parent[a] = b
        elif rank[a] > rank[b]:
            parent[b] = a
        else:
            parent[b] = a
            rank[a] += 1
시간 복잡도

아커만 함수의 역함수를 시간복잡도로 가진다
=> 대충 ==O(logN)==와 유사하다고 한다.

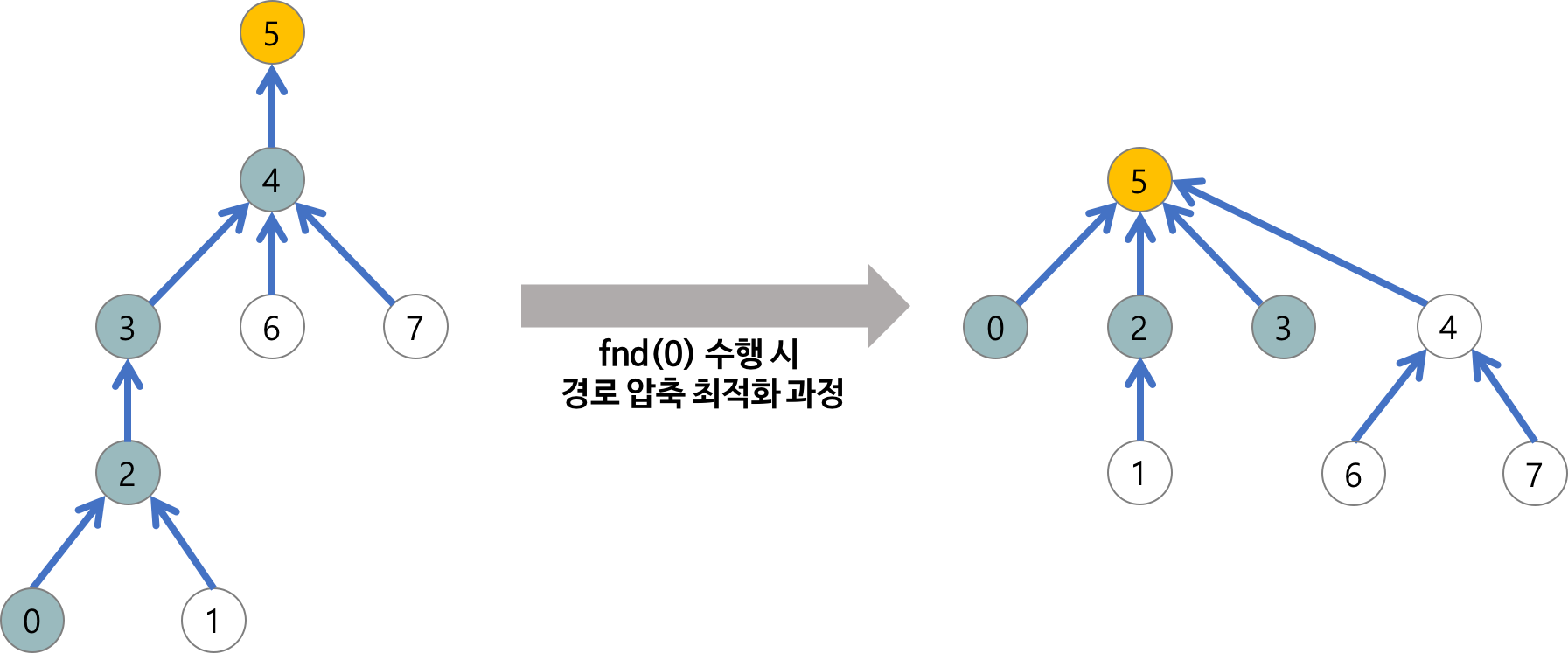
경로압축(path compression)

Disjoint set은 집합이기 때문에 우리는 경로를 기억할 필요가 없다.
=> 경로를 지우고 곧장 루트 노드로 연결시켜서 경로를 줄인다.

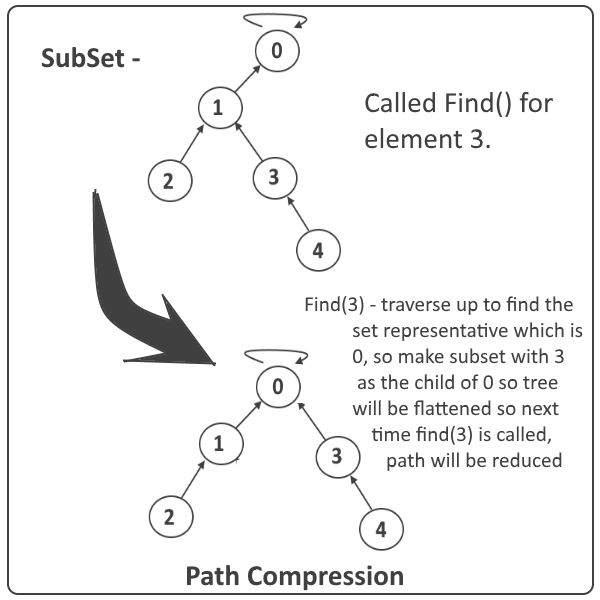
378334b263699b75513554fd2f8870e7_MD5.jpg
그림에서 find(3)을 진행하면서 루트 노드인 0을 3의 부모노드로 바꾸면서 경로 압축을 할 수 있다.

코드
def find(x):
    y = x
    while y != parent[y]:
        y = parent[y]
    parent[x] = y
    return y

def union(x, y):
    parent[find(y)] = parent[find(x)]

Union by rank vs path compression

미세하게 union by rank가 더 빨랐다.
백준 1717번 참고

두가지 다 적용했을 때도 차이가 없어서 문제를 풀때는 한가지만 적용해서 푸는게 효율적일 것 같다.

그리고 경로 압축이 더 코드가 간결하다
=> 경로 압축으로 하자

references