LCS
최장 공통 부분수열 vs 최장 공통 문자열
LCS라 하면 주로 최장 공통 부분수열(Logest Common Subsequence)를 말하지만, 최장 공통 문자열(Logest Common Substring)을 말하기도 한다.
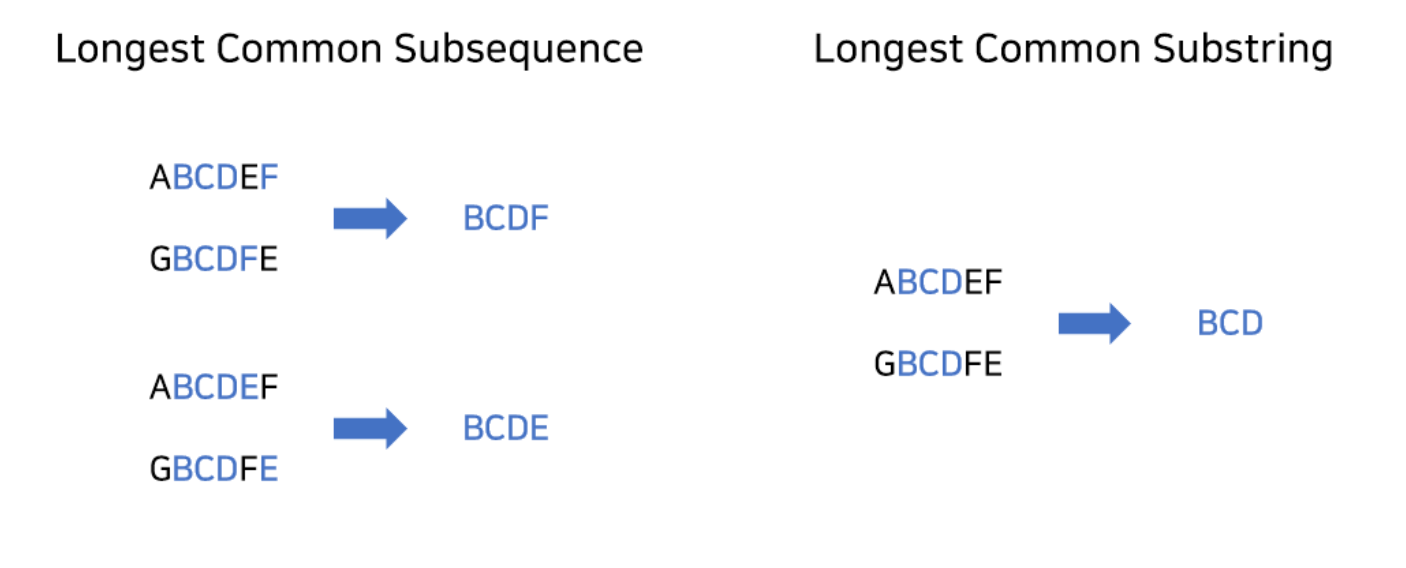
최장 공통 부분수열 (Longest Common Subsequence, LCS)
- 두 문자열에서 순서는 유지되지만 연속적일 필요는 없는 가장 긴 부분수열을 찾는 문제입니다.
최장 공통 문자열 (Longest Common Substring)
- 두 문자열에서 연속적으로 일치하는 가장 긴 부분 문자열을 찾는 문제입니다.
두 경우 모두 이전의 최댓값을 기반으로 찾기 때문에 Dynamic Programming 사용하여 해결할 수 있다.
Logest common Substring
점화식
A[i-1] == B[j-1]이면
dp[i][j] = dp[i-1][j-1] + 1
A[i-1] != B[j-1]이면
dp[i][j] = 0
공통 문자열은 연속되어야한다. 그래서 두 문자의 앞 글자까지의 공통 문자열이 있다면 계속 연속으로 이어지기 때문에 위와 점화식이 나온다.
과정
문자열 A, B 의 최장 공통 문자열을 구한다고 했을 때
- 두 문자열의 각 문자를 비교
- 문자가 같으면
dp[i][j] = dp[i-1][j-1] + 1로 업데이트 - 문자가 다르면
dp[i][j] = 0으로 설정 - DP 테이블에서 최댓값을 찾고, 해당 위치에서 문자열을 추출
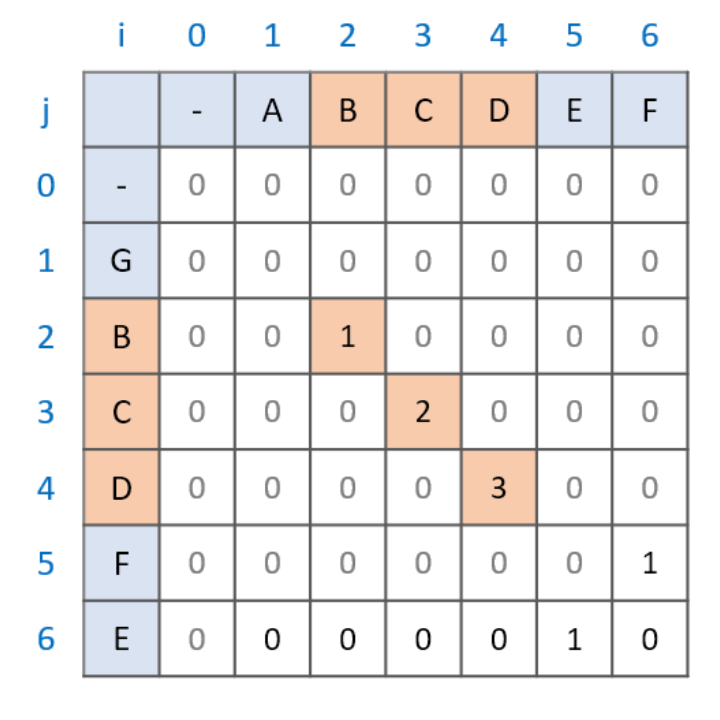
ABCDEF 와 GBCDFE 의 공통 문자열을 구하는 경우 DP 배열이 아래와 같은 결과를 갖는다.
DP 배열의 최댓값이 최장 공통 문자열의 길이가 된다.
출처
코드
def longest_common_substring(A, B):
m, n = len(A), len(B)
dp = [[0] * (n+1) for _ in range(m+1)]
max_length = 0
end_pos = 0
for i in range(1, m+1):
for j in range(1, n+1):
if A[i-1] == B[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
if dp[i][j] > max_length:
max_length = dp[i][j]
end_pos = i
else:
dp[i][j] = 0
return A[end_pos - max_length:end_pos]
A = "ABCDF"
B = "BCDE"
print("Longest Common Substring:", longest_common_substring(A, B))
Longest Common Subsequence
점화식
A[i-1] == B[j-1]이면
dp[i][j] = dp[i-1][j-1] + 1
A[i-1] != B[j-1]이면
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
- 문자가 같지 않으면 이전 문자열까지의 최대값을 가져오면 되기 때문에
max(dp[i-1][j], dp[i][j-1]) - 문자가 같으면 각 문자 이전에 최댓값에 +1
과정
- 두 문자열의 각 문자를 비교
- 문자가 같으면
dp[i][j] = dp[i-1][j-1] + 1 - 문자가 다르면
dp[i][j] = max(dp[i-1][j], dp[i][j-1]) - 마지막 dp 값이 최장 길이
ABCDEF 와 GBCDFE 의 예시
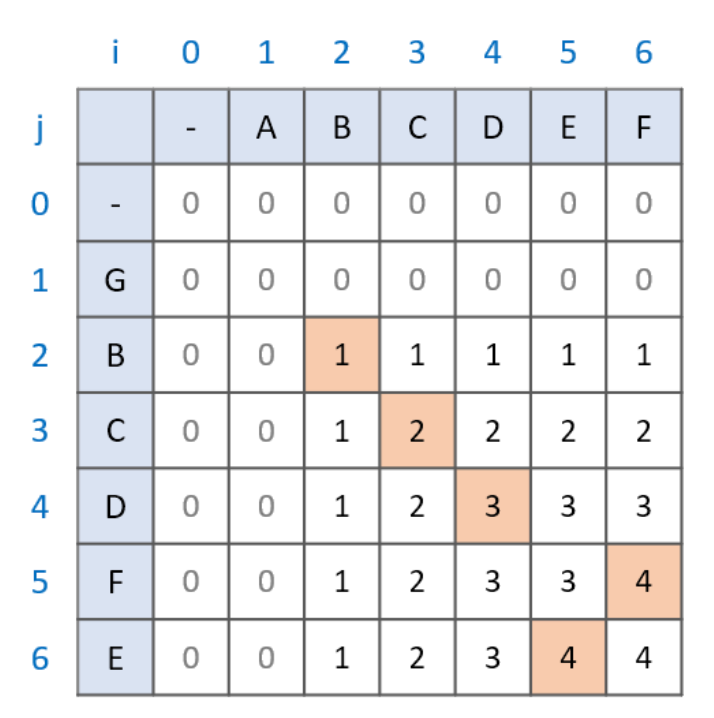
코드
def longest_common_subsequence(A, B):
m, n = len(A), len(B)
dp = [[0] * (n+1) for _ in range(m+1)]
for i in range(1, m+1):
for j in range(1, n+1):
if A[i-1] == B[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[m][n]
A = "ABCDF"
B = "ACDF"
print("Longest Common Subsequence Length:", longest_common_subsequence(A, B))
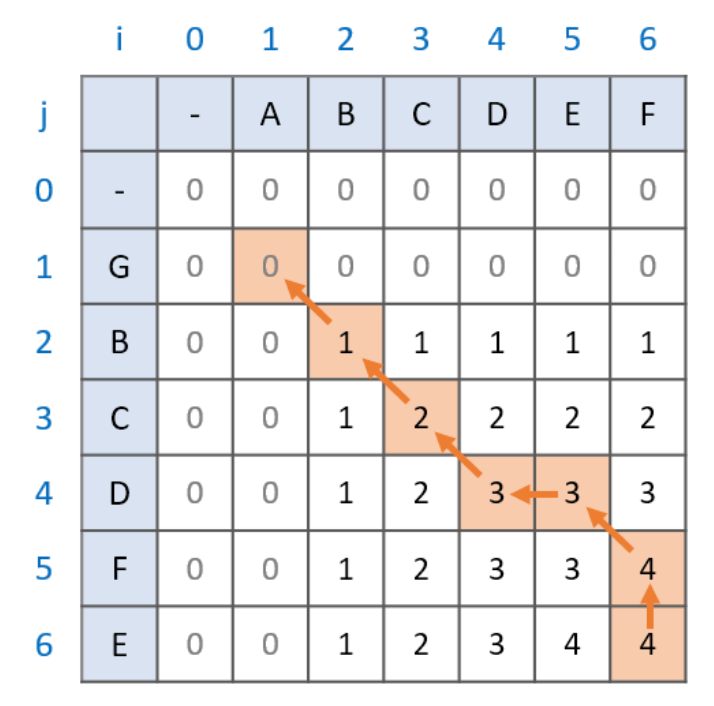
역추적
최장 공통 부분수열은 공통 문자열과 다르게 부분수열을 찾는게 조금 복잡하다.
문자열이 달라도 이전 최댓값을 가져오기 때문에
dp[i-1][j], dp[i][j-1]중에 같은 값으로 이동- 같은 값이 없으면
dp[i-1][j-1]로 이동 - 이동할 수 없거나,
코드
def lcs_backtracking(A, B):
m, n = len(A), len(B)
dp = [[0] * (n+1) for _ in range(m+1)]
for i in range(1, m+1):
for j in range(1, n+1):
if A[i-1] == B[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
lcs = []
i, j = m, n
while i > 0 and j > 0:
if A[i-1] == B[j-1]:
lcs.append(A[i-1])
i -= 1
j -= 1
elif dp[i-1][j] > dp[i][j-1]:
i -= 1
else:
j -= 1
return ''.join(reversed(lcs))
A = "ABCDF"
B = "ACDF"
print("Longest Common Subsequence:", lcs_backtracking(A, B))
역추적 조건을 백준 9252번 - LCS 2#정답 코드 에서 처럼 dp값이 0 인지 체크할 수도 있다.
관련 문제
Reference
- emplam27 - [알고리즘] 그림으로 알아보는 LCS 알고리즘 (LCS 설명이 그림으로 정말잘되어 있다)