B-Tree
B-Tree란
트리의 일종으로 이진트리를 확장해 하나의 노드가 자식 노드를 2개 이상 가질 수 있는 트리 구조이다.
이진 트리는 아니지만 모든 리프노드들이 같은 레벨을 가질 수 있도록 스스로 균형을 맞춘다는 점에서 균형 이진 트리와 비슷하다.
실제 DB의 인덱싱에서 사용된다고 알려져 있으나, B트리에서 발전한 B+Tree를 사용한다고 한다.
B-Tree의 조건
앞서서 몇가지 용어 정리를 하고 넘어가겠다.
- 각 노드안의 데이터를 key라고 한다.
- 리프노드가 아닌 노드를 내부 노드라고 한다.
- 포인터는 자식노드들을 가르킨다.
노드에 한개의 데이터(key)를 가지는 일반적인 트리와 달리 B-Tree는 한 노드에 2개 이상의 데이터가 들어갈 수 있다.
최대 M개의 자식을 가질 수 있는 M차 B트리는 아래의 조건들을 만족한다.
노드는 [M/2]-1 에서 M-1 개의 key값을 가질 수 있다.
최소 [M/2]-1 개라는 조건은 key 갯수가 M에 도달하면 나누어지기 때문이다.
노드 삽입 과정을 보면 이해가 된다.
5차 B트리 예시
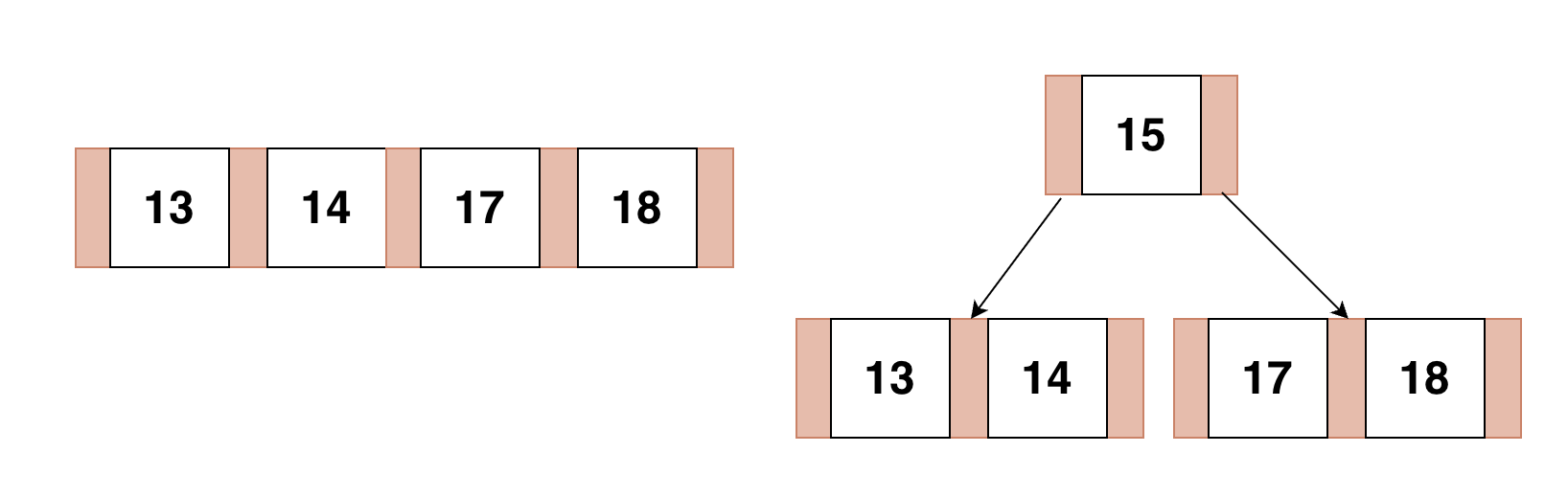
노드의 key 갯수가 K 일 때, 자식 노드의 갯수는 K+1이다.
즉 리프노드가 아니라면, 각 포인터들이 1개의 자식노드를 가르켜야한다.
왼쪽 포인터는 key보다 작은 값을, 오른쪽 포인터는 Key 보다 큰값을 가르킨다.
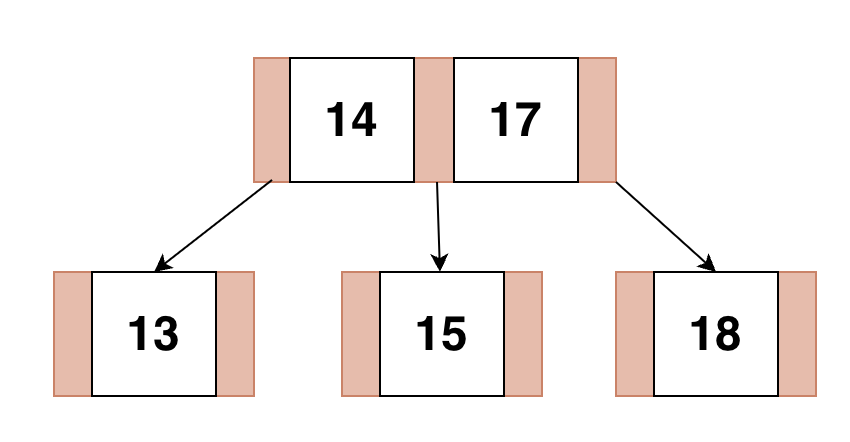
모든 리프 노드들이 같은 레벨에 존재한다.
모든 리프 노드들이 같은 레벨에 존재해야한다.
루트 노드에서 모든 리프토드로 가는 경로의 길이가 같다.
B-Tree 탐색
루트노드에서 시작하여 하향식으로 검색을 수행한다.
검색하고자하는 key를 k라고 했을 때, 검색 과정은 다음과 같다.
- 루트 노드에서 시작하여 key들을 순회하면서 검사
- K와 key값 대소 비교해서 서브트리 찾아 내려감
- 1과 2번 과정을 리프 노드에 도달할 때 까지 반복
9를 찾는 과정(일일히 만들기 너무 귀찮다)
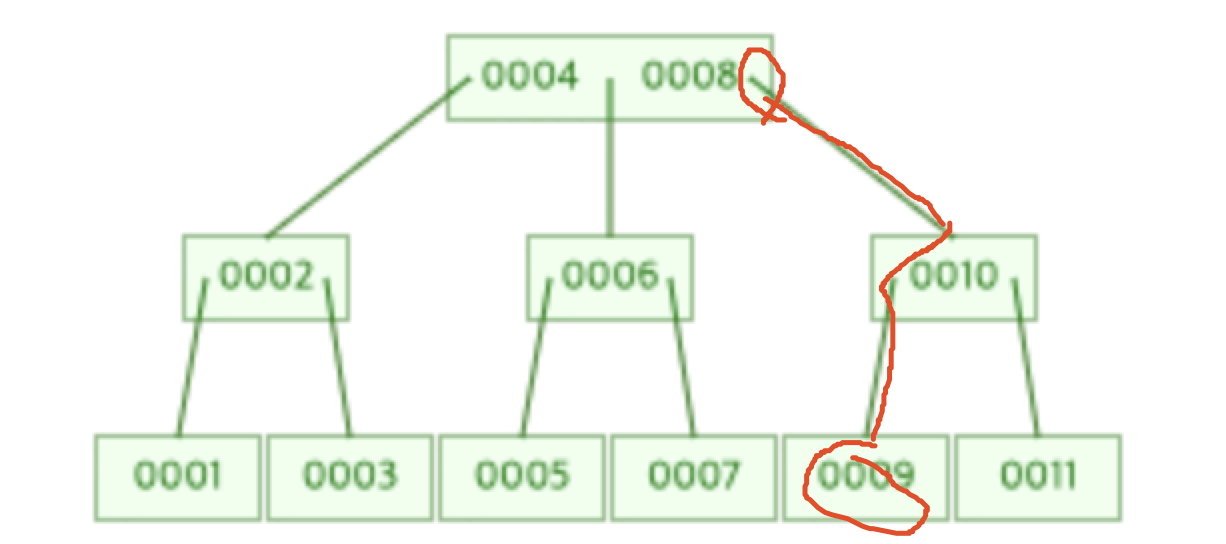
B-Tree 삽입
삽입은 상향식으로 진행된다.
삽입은 항상 리프 노드에서 시작된다.
- key 넣을 적절한 리프노드 탐색. [[#B-Tree 탐색]]과 동일
- 리프노드에 key 삽입
- 리프노드의 key 갯수가 최대치를 넘어가면 [[#분리]]
3차 B트리를 기준으로 작성했다.
분리
리프노드의 Key 갯수가 최대치를 초과하는 경우 분리가 필요하다.
- 중앙값을 분리하여 부모노드로 병합 or 새로 생성
- 왼쪽 key를 중앙값의 왼쪽 자식, 오른쪽 Key를 중앙값의 오른쪽 자식으로 설정
- 부모 노드도 분할이 필요한지 검사 후 반복
다음과 같이 4가 삽입되어서 분리가 필요해졌다.
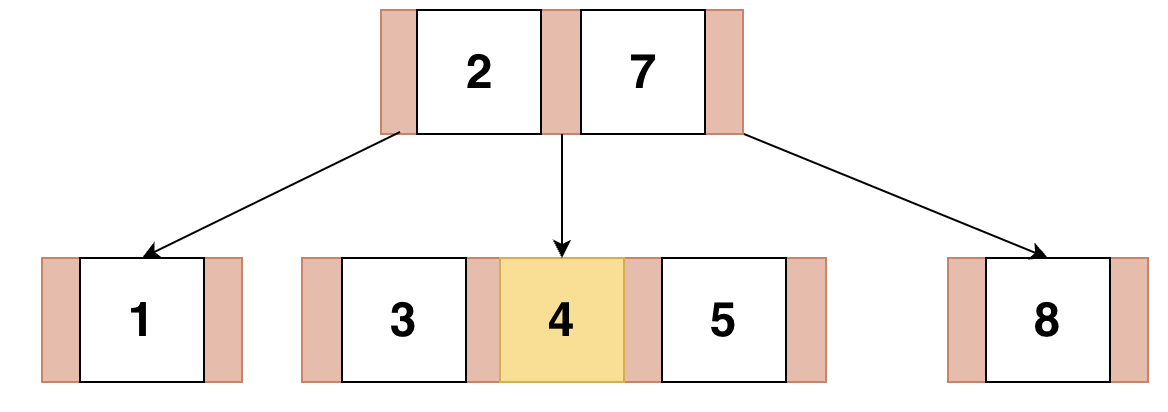
중앙 Key를 부모노드와 병합하고 기존 Key들을 자식으로지정
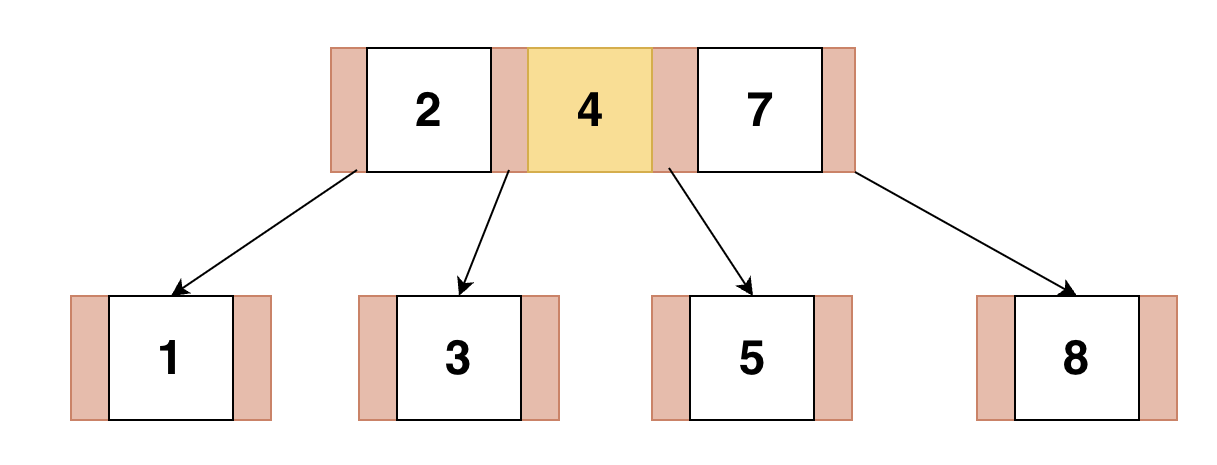
또 다시 루트 노드의 Key가 가득 찼기 때문에 분리 실행
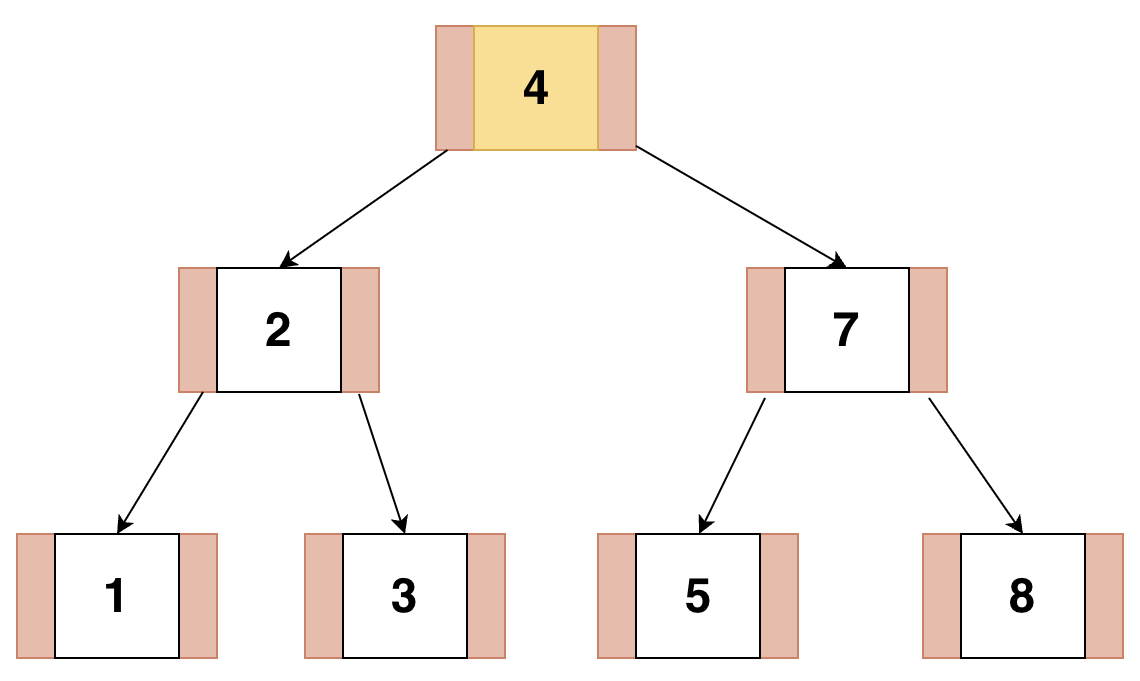
이제 모든 노드들이 안정한 상태에 있으므로 삽입을 종료한다.
B-Tree 삭제
요소를 삭제하는 과정은 다음과 같다.
- 삭제할 키가 있는 노드검색
- 키 삭제
- 필요한 경우, 트리 균형 조정
즉, 일반적인 트리에서의 삭제와 같으나, [[#B-Tree의 조건]]을 만족하지 못할 경우 트리 균형을 조정해준다.
Lmax : 현재 노드의 왼쪽 자식들 중 가장 큰 key
Rmin : 현재 노드의 오른쪽 자식들 중 가장 작은 key
Parent : 현재 노드를 가르키는 부모 노드의 자식
K : 삭제할 key
3차 트리에서의 삭제 과정에서 일어날 수 있는 삭제 Case들을 나누어 각각의 경우에서 어떤 방법으로 균형을 조정할 수 있는지 알아보자.
Case 1. 리프 노드에서의 삭제
if 리프 노드를 제거해도 최소 개수를 만족하는 경우
해당 노드를 바로 삭제해준다.
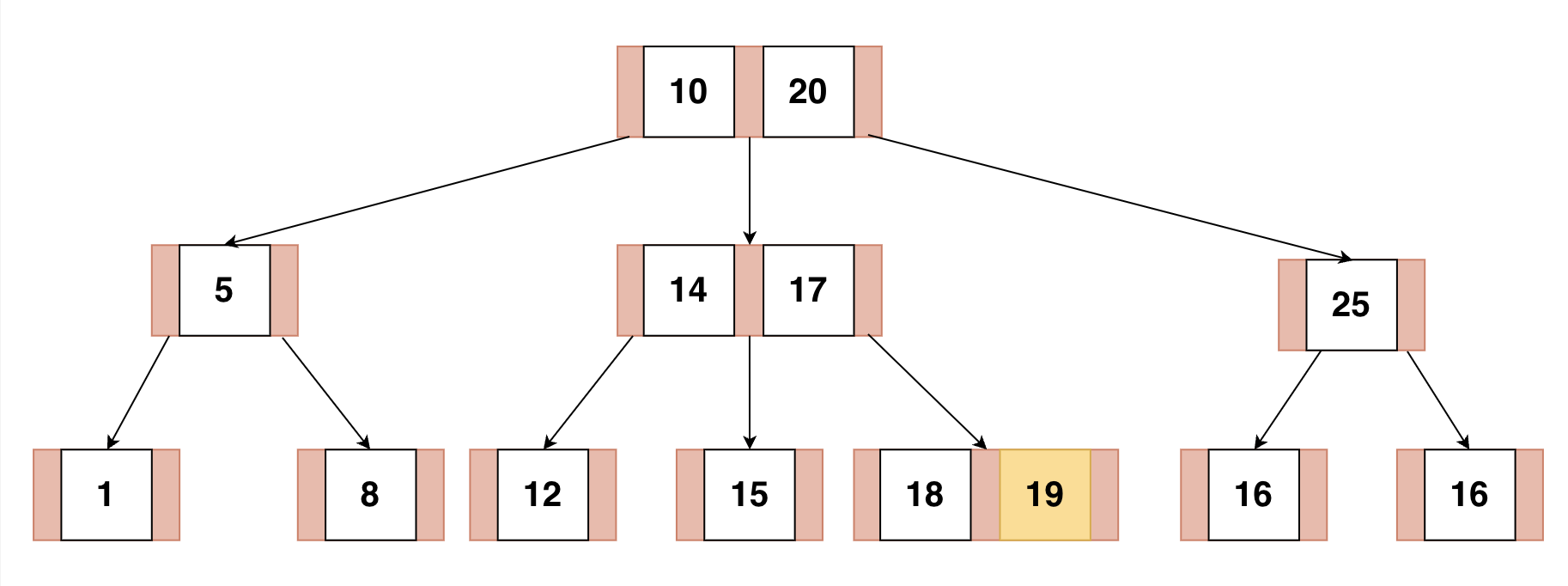
19번 노드를 삭제해줘도 B 트리의 조건을 만족하므로 간단하게 삭제해준다.
else if 최소 개수를 만족하지 못하지만, 형제 노드가 여유로운 경우
형제 노드에서 1개를 선택하여 Parent와 변경한다.
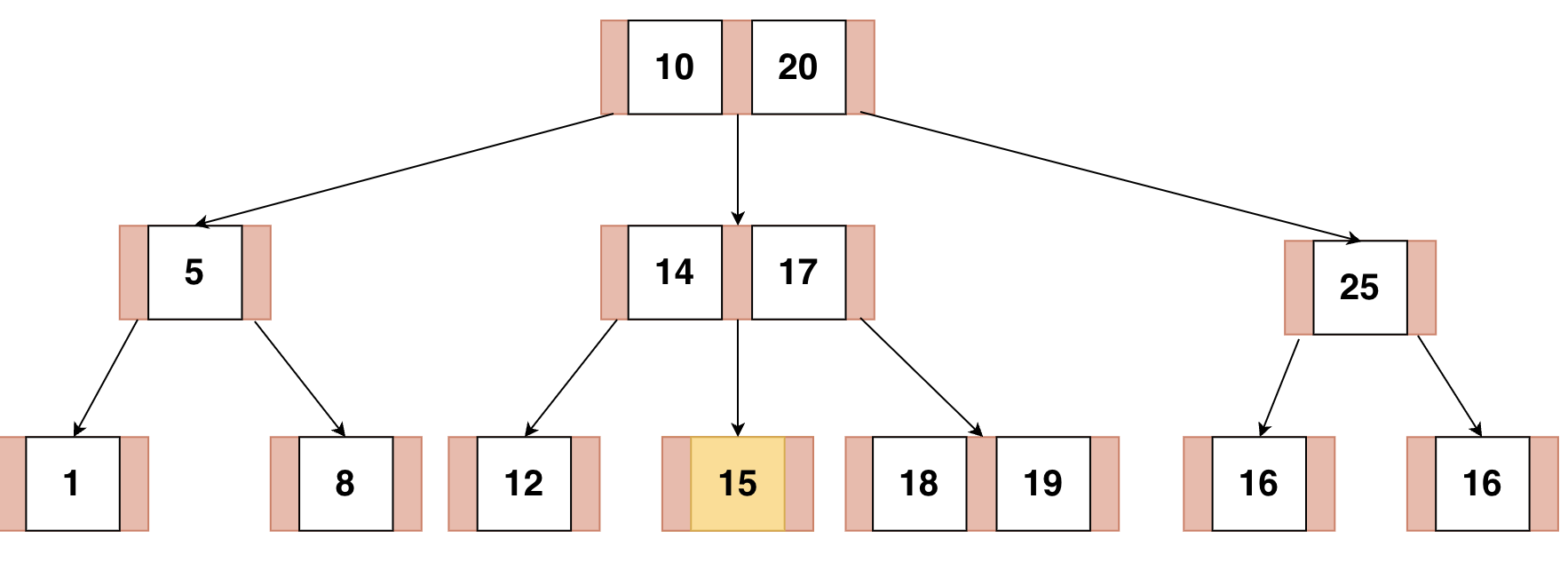
값 15를 제거하는 경우, 형제 노드인 18,19에서 18이 Parent가 되고 parent였던 17이 제거된 노드 자리에 위치한다.
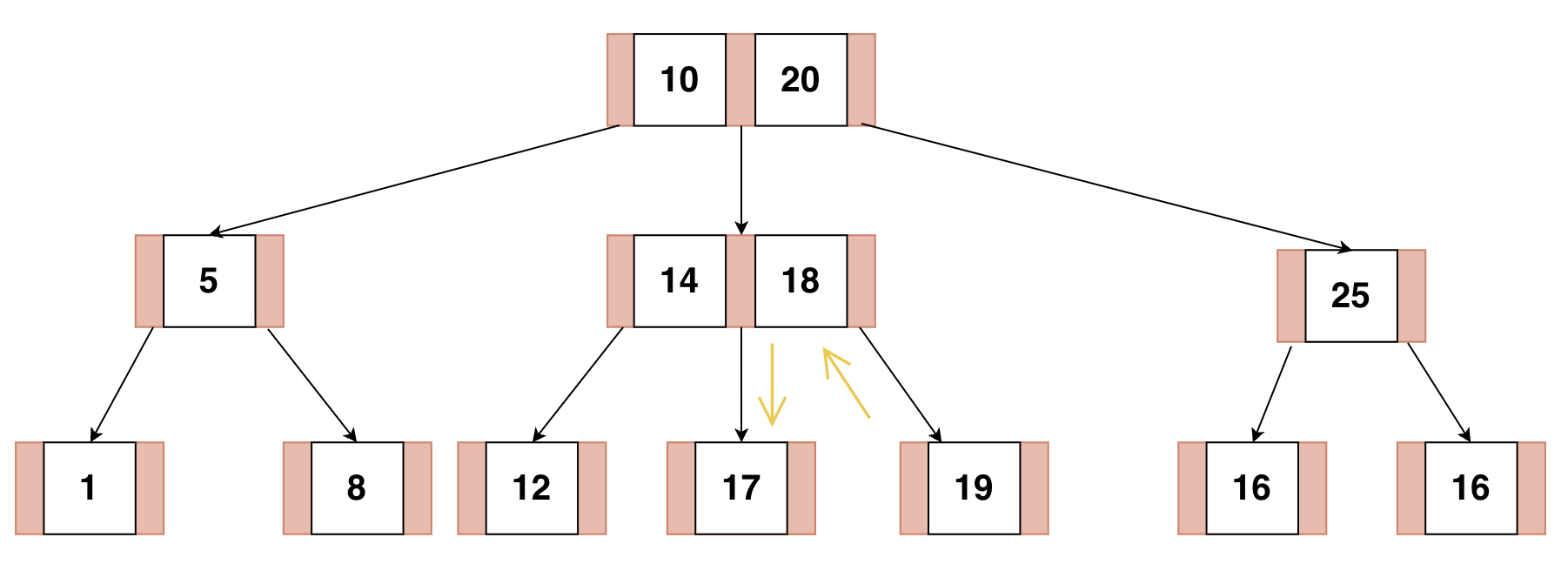
else if 부모 노드를 분할할 수 있을 때
부모 노드를 자식으로 병합한다.
19번 노드를 제거하는 경우
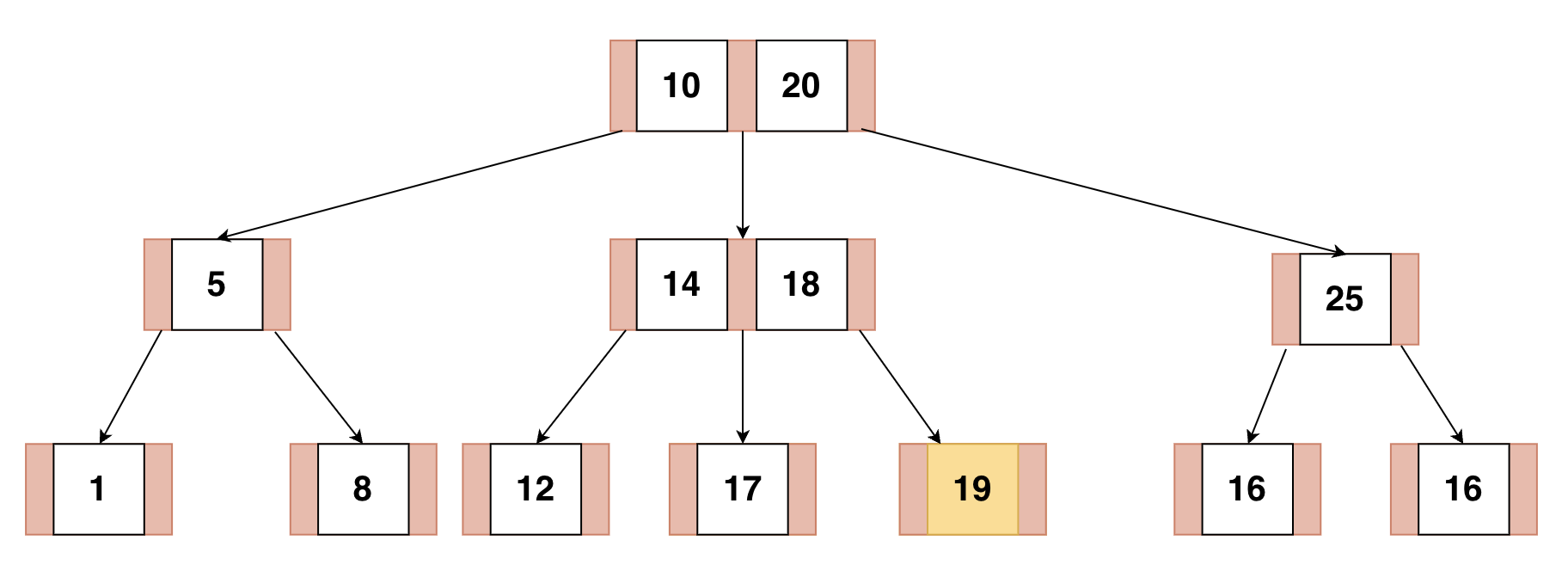
부모노드를 자식으로 병합하여 이를 해결할 수 있다.
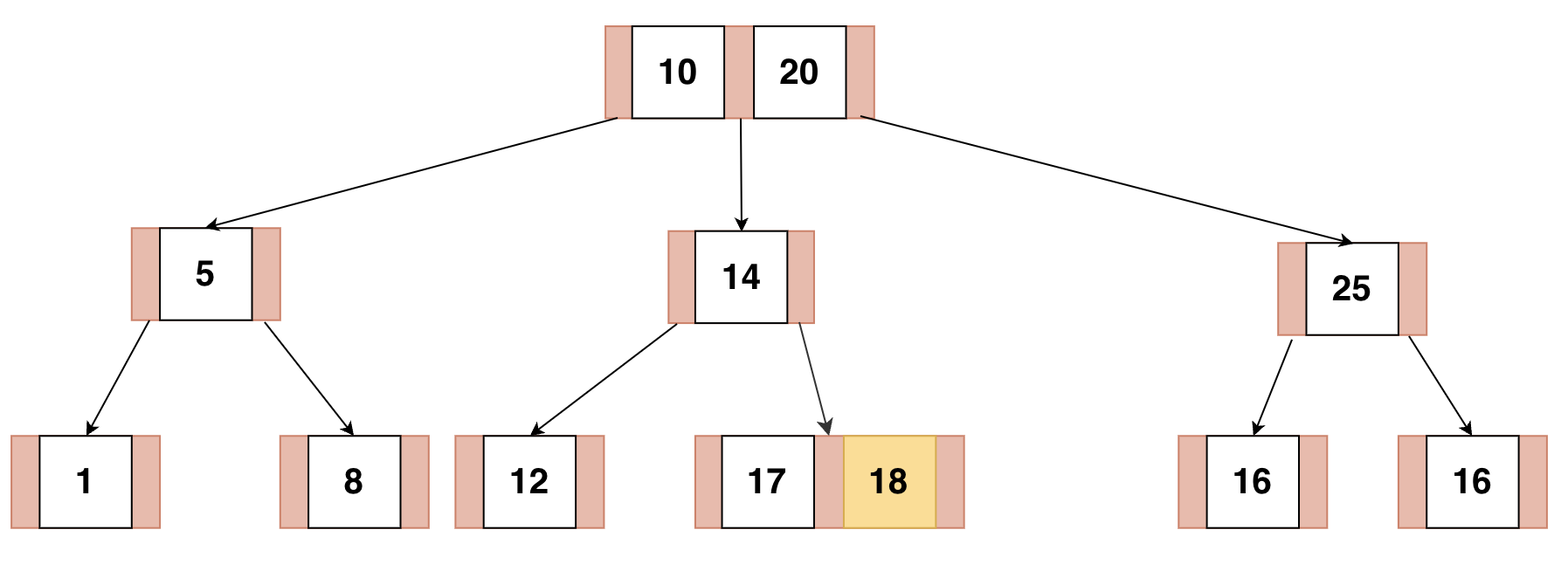
else 아무것도 못할 때,
이 경우는 트리의 재구조화가 필요하다.
[[#삭제 후, 현재 노드와 자식 노드 모두 Key 개수가 최소인 경우]] 에서의 트리 재구조화 참고.
Case 2. 리프노드가 아닌 내부 노드에서 삭제
삭제 후, 자식 노드의 최소 유지 개수보다 큰 경우
K의 Lmax 혹은 Rmin과 자리를 바꾼다.
이후에는 리프노드에서의 삭제와 동일
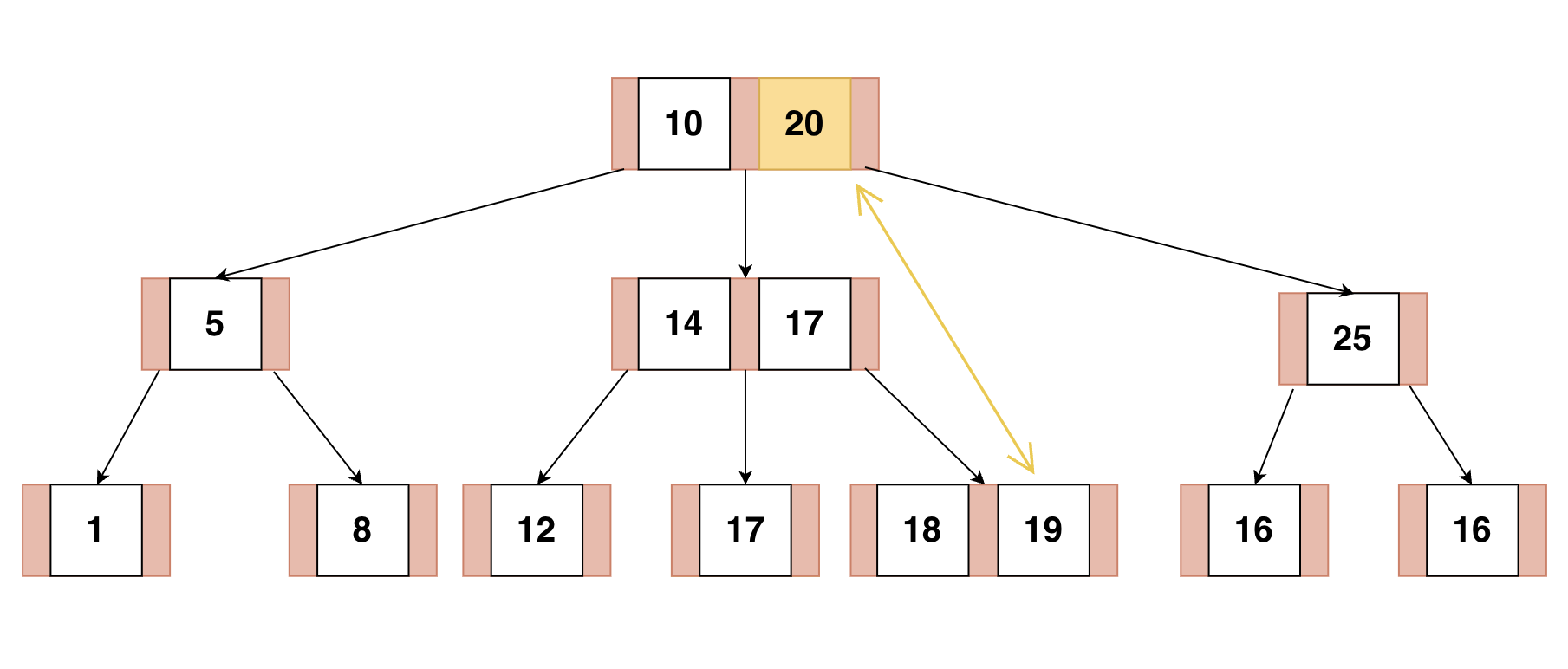
위와 같이 Lmax인 노드와 값을 바꾼 뒤, 삭제를 진행하면 된다.
삭제 후, 현재 노드와 자식 노드 모두 Key 개수가 최소인 경우
이 경우에는 K 노드를 리프 노드로 보낼 수 없기 때문에, 트리의 재구조화가 필요하다.
- K 삭제하고, K의 자식들을 하나로 합친다. 이를 N1 이라고하자.
- K의 Parent를 K의 형제 노드에 합친다. 이를 N2 라고 하자.
- N1을 N2의 자식으로 입양시킨다.
- N2의 key에 따라서 분할 하거나, 2번과정 반복
- key 수가 최대 개수를 넘어가면 [[#B-Tree 삽입]] 에서처럼 분할을 해준다.
- Key수가 최소 유지 개수 보다 작다면 N2를 K로 치환하여 2번 과정부터 반복
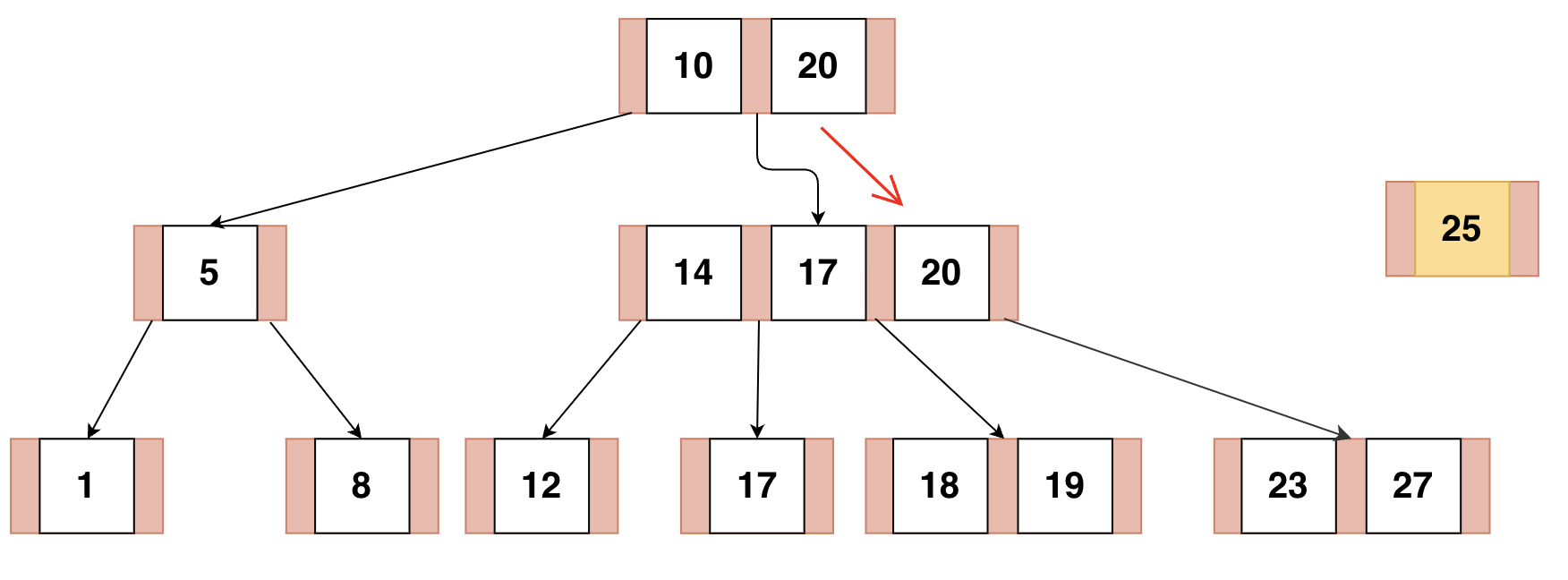
25번 노드를 제거 하는 경우 위와 같이 된다.
이후 14,17,20 노드를 분할해주면 된다.
+ 추신
글을 작성하고 보니 가장 오른쪽 리프 노드의 값이 잘못 설정되어 있었다...
하지만 내용을 이해하는데에는 문제가 없고 다이어그램을 다시 만들어서 캡쳐하는 것은 너무 귀찮은 작업이므로 넘어가주길 바란다ㅠ