트리
트리는 계층적인 구조로 데이터를 나타내는 자료구조이다.
루트 노드에서 시작해서 여러 노드로 이어져 구성된다. 각 노드는 값과 자식 노드를 가질 수 있다.
모양이 꼭 나무를 거꾸로 한 모습이라고 해서 트리라고 지어졌다고 한다.
트리 용어
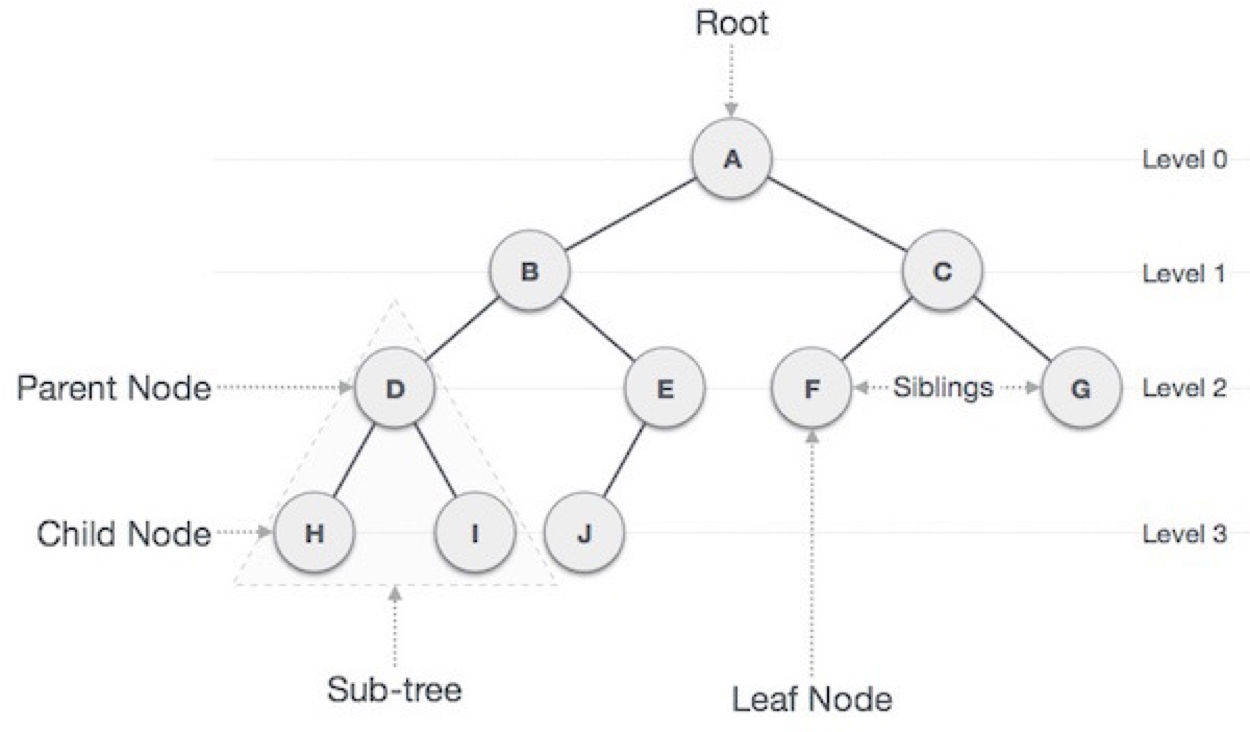
- root node : 부모가 없는 노드, 태초의 노드. 박혁거세 노드
- leaf node : 단말노드, 자식이 없는 노드, 박응애 노드
- internal node : 단말 노드가 아니니 노드
- edge : 노드를 연결하는 선 (=link)
- sibling : 형제, 같은 부모를 가지는 노드
- size : 자신을 포함한 자손 노드의 개수
- depth : 루트에서 어떤 노드까지의 간선 수
- level : 같은 depth인 노드의 집합
- degree : 차수, 노드의 자식 수
- degree of tree : 트리의 최대 차수
트리의 특징
- 대상 정보의 각 항목들을 계층적으로 구조화할 때 사용하는 비선형 자료구조 이다.
- 저장보다 효율적인 탐색을 위해 사용 된다.
- 부모와 자식의 계층적인 관계로 표현된다.
- 트리는 사이클이 없다.
- 루트 노드를 제외한 모든 노드는 단 하나의 부모노드를 가진다.
트리 순회
트리의 모든 노드를 방문하는 방법을 트리 순회라고 합니다. 대표적으로는 전위 순회(pre-order traversal), 중위 순회(in-order traversal), 후위 순회(post-order traversal)가 있습니다. 각각의 방법은 루트 노드를 언제 방문하느냐에 따라 결정됩니다.
이진 트리
트리를 구성하는 노드의 자식이 최대 두개인 트리. 자식의 수가 0,1,2 중 하나이다.
- 두개의 자식 노드 중에서 왼쪽 노드를
left node, 오른쪽 노드를right node라고 한다.
이진 트리 종류
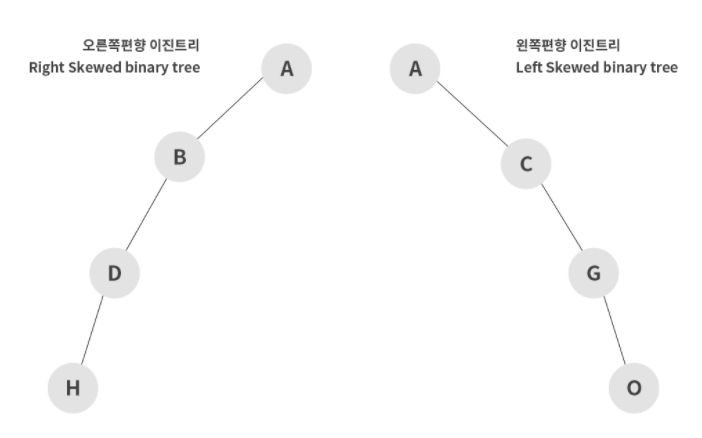
Skewed binary tree(편향 이진 트리)
한쪽으로만 편향된 트리.
왼쪽이나 오른쪽 서브트리만 가진 트리를 말한다.
→ 탐색시 비효율
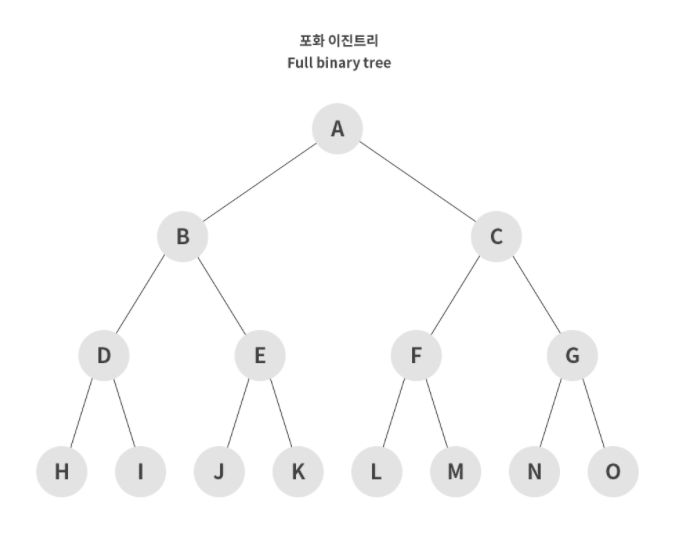
Full BInary Tree(포화 이진 트리)
leaf node를 제외한 모든 노드의 차수가 2개로 이루어져있는 트리.
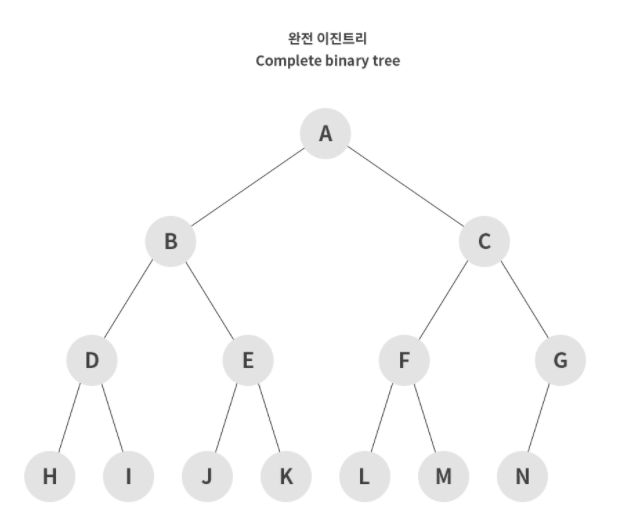
Complete Binary Tree(완전 이진 트리)
포화 이진 트리와 비슷한데 모든 노드가 왼쪽 부터 생성되는 이진트리라고 한다.
뭐가 다른지 모르겠다.
이진 트리의 순회
트리의 모든 모드를 거치는 과정을 순회라고 한다.
순회 구현에 사용되는 트리와 node 코드이다.
class Node(object):
def __init__(self, item):
self.item = item
self.left = self.right = None
class BinaryTree(object):
def __init__(self):
self.root = None
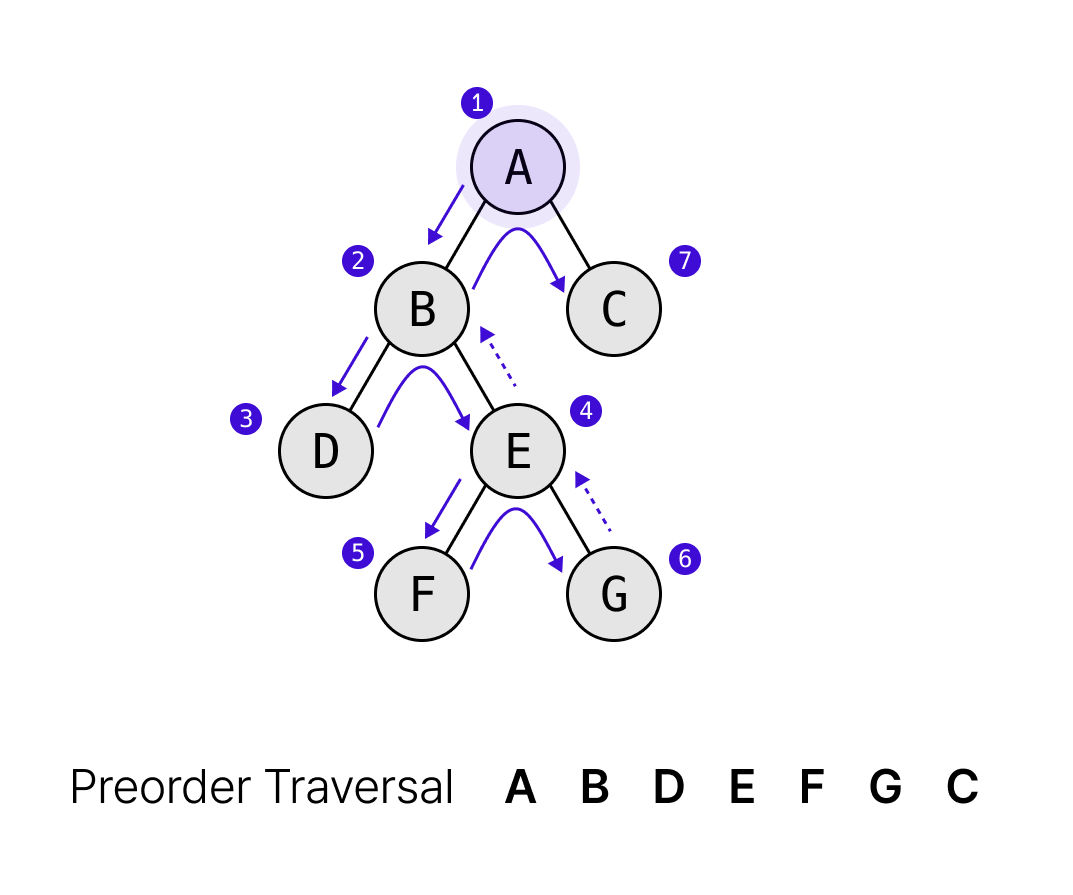
전위 순회(Preorder Traversal)
루트 → 왼쪽 서브트리 → 오른쪽 서브트리
def preorder(n) :
if n is not None :
print(n.data, end=' ')
preorder(n.left)
preorder(n.right)
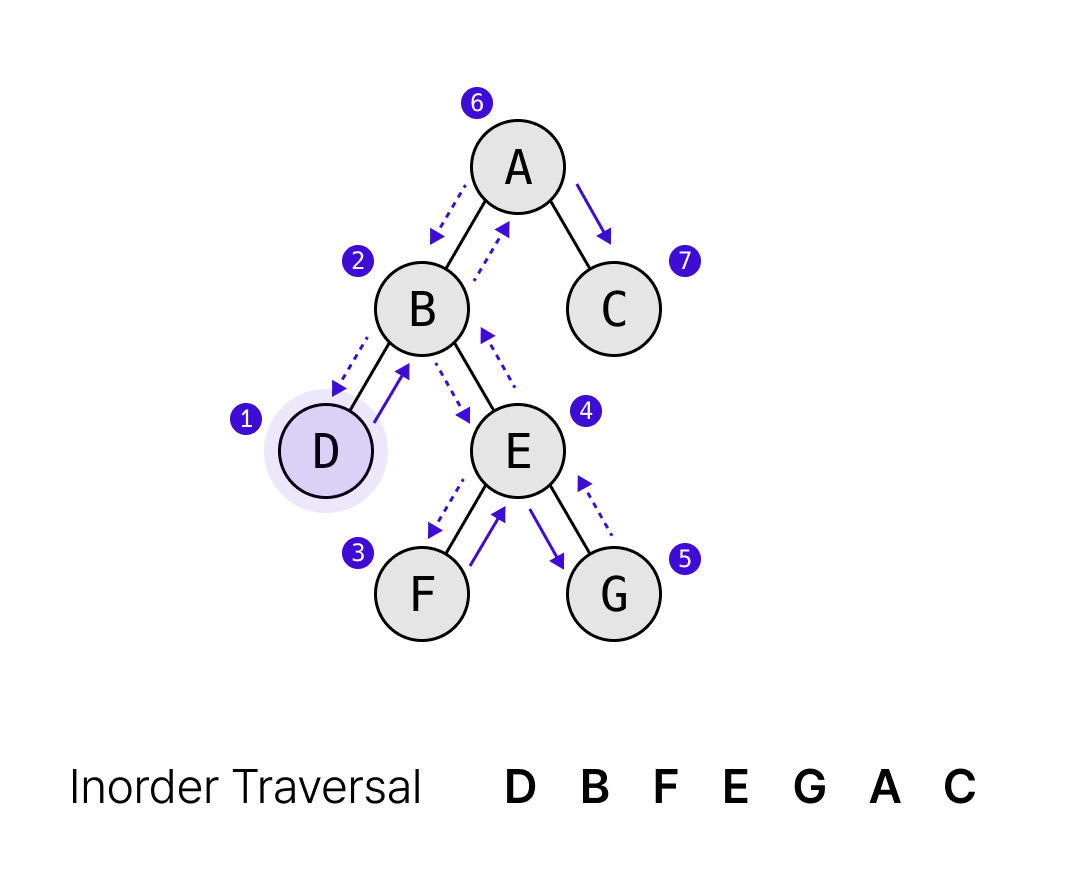
중위 순회(Inorder Traversal)
왼쪽 서브트리 → 루트 → 오른쪽 서브트
def inorder(n) :
if n is not None :
inorder(n.left)
print(n.data, end=' ')
inorder(n.right)
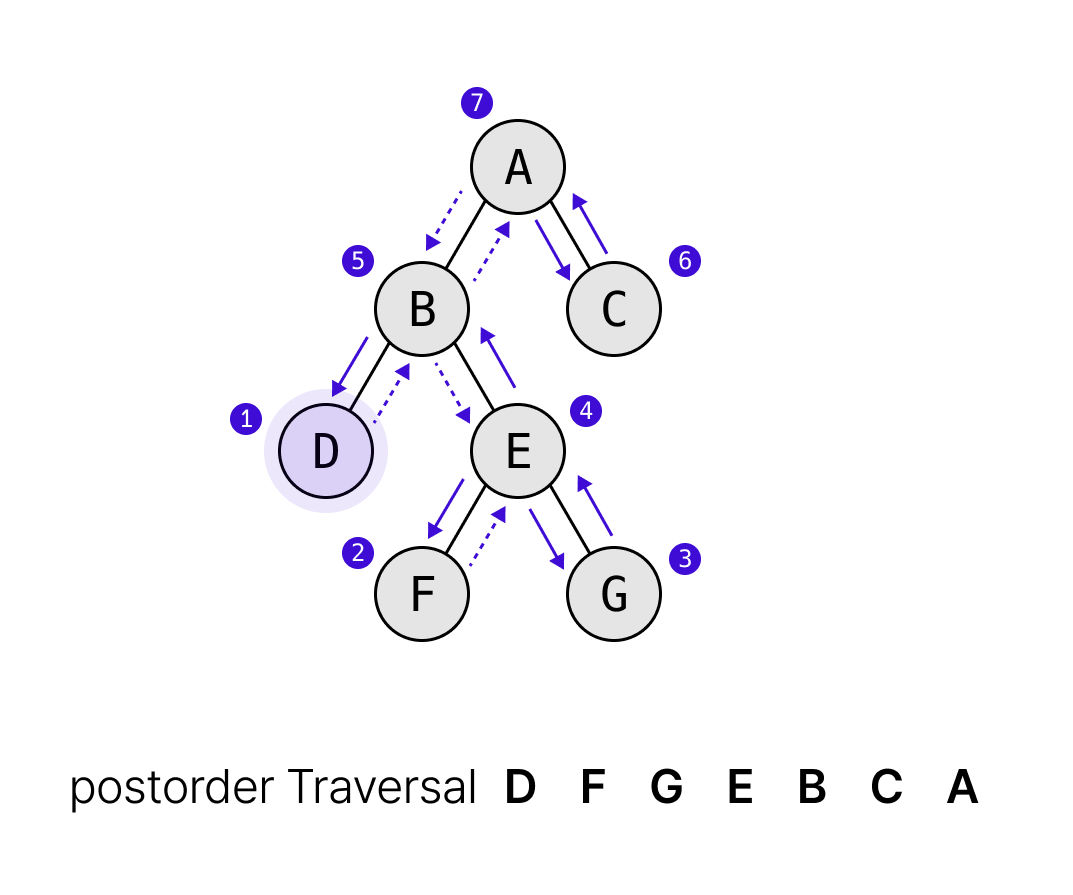
후위 순회(Postorder Traversal)
왼쪽 서브트리 → 오른쪽 서브트리 → 루트
def postorder(n) :
if n is not None :
postorder(n.left)
postorder(n.right)
print(n.data, end=' ')
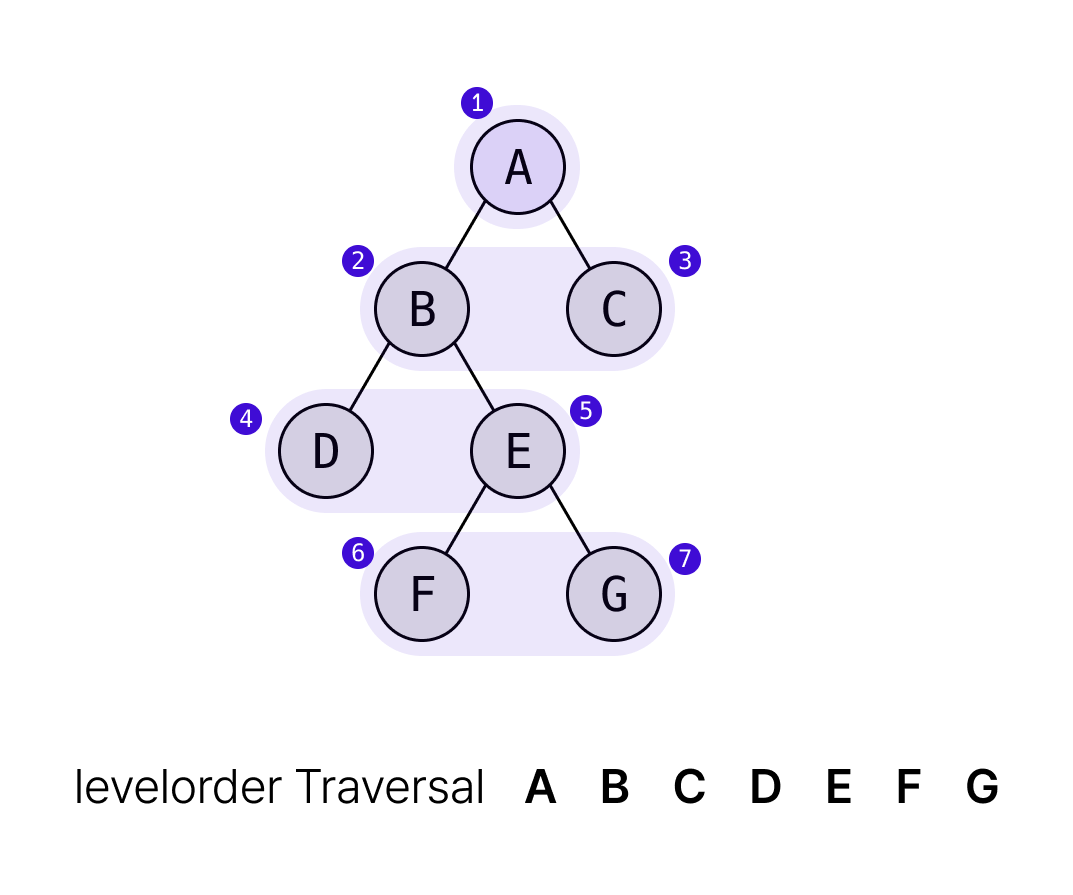
레벨 순회(Level Traversal)
낮은 레벨부터 탐색하는 방법이다.
queue를 이용하는 방식으로 주로 구현한다.
def levelorder(root) :
queue = deque()
queue.enqueue(root)
while not queue.isEmpty() :
n = queue.dequeue()
if n is not None :
print(n.data, end=' ')
queue.enqueue(n.left)
queue.enqueue(n.right)
이진 탐색 트리
이진 탐색과 연결리스트를 결합한 자료구조의 일종. 이진탐색에 트리를 적용하여 빠른 탐색과 빈번한 자료 입력과 삭제를 가능하게 위해 고안되었다고 한다.
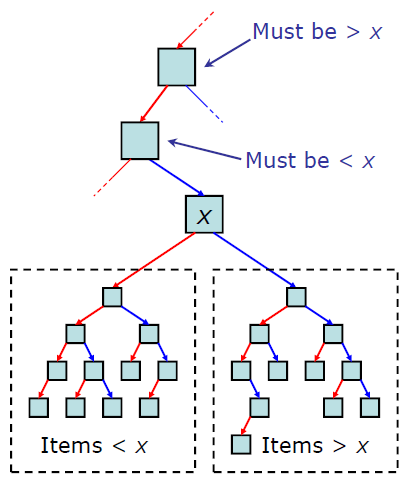
이진탐색 트리의 조건
- 부모를 기준으로 작으면 왼쪽 서브트리 크면 오른쪽 서브트리에 위치한다.
- 중복된 노드가 없어야한다.
- 서브트리 또한 이진탐색 트리이다.
연산
이진 트리의 핵심 연산으로 검색, 삽입, 삭제가 있다.
기본 node와 binarySearchTree의 틀은 아래와 같다.
class Node:
def __init__(self, val):
self.val = val
self.leftChild = None
self.rightChild = None
class BinarySearchTree:
def __init__(self):
self.root = None
def setRoot(self, val):
self.root = Node(val)
검색
- 검색하려는 값과 노드 비교
- 찾는 값이 작으면 왼쪽 서브트리, 크면 오른쪽 서브트리에서 검색
def find(self, val):
if (self.findNode(self.root, val) is False):
return False
else:
return True
def findNode(self, currentNode, val):
if (currentNode is None):
return False
elif (val == currentNode.val):
return currentNode
elif (val < currentNode.val):
return self.findNode(currentNode.leftChild, val)
else:
return self.findNode(currentNode.rightChild, val)
삽입
서브트리의 이진트리 속성이 깨지지 않기 위해서 삽입은 항상 leaf node에서 이루어진다.
→ 트리의 불균형을 만들 수 있다.
⇒ 트리의 탐색은 트리의 깊이에 영향을 받기 때문에 효율이 떨어진다.
def insert(self, val):
if (self.root is None):
self.setRoot(val)
else:
self.insertNode(self.root, val)
def insertNode(self, currentNode, val):
if (val <= currentNode.val):
if (currentNode.leftChild):
self.insertNode(currentNode.leftChild, val)
else:
currentNode.leftChild = Node(val)
elif (val > currentNode.val):
if (currentNode.rightChild):
self.insertNode(currentNode.rightChild, val)
else:
currentNode.rightChild = Node(val)
삭제
삭제의 경우 3가지 케이스가 존재한다.
자식노드가 0,1,2개 인 경우 이다.
-
자식노드가 없는 경우
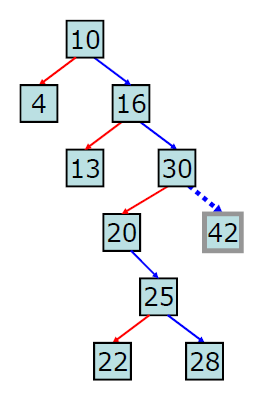
이 경우 에는 그냥 삭제해 주면 된다.
-
자식 노드가 1개인 경우(외동노드)
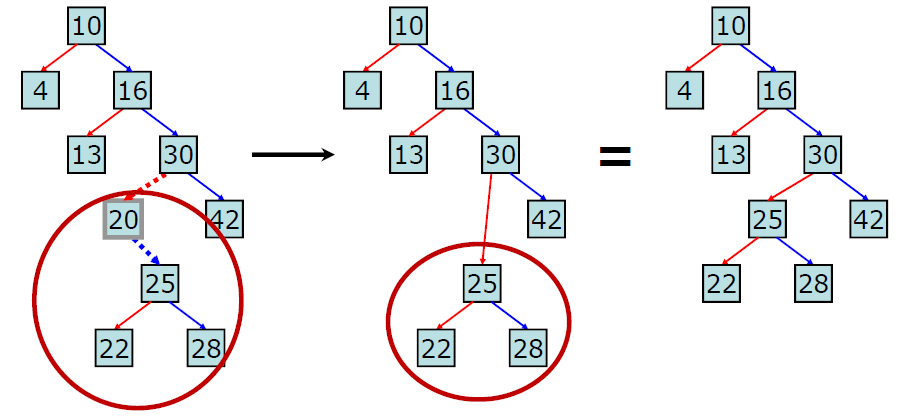
이 경우에는 삭제 노드의 부모 노드와 그 외동노드와 연결해 주면 된다. -
자식 노드가 2개인 경우
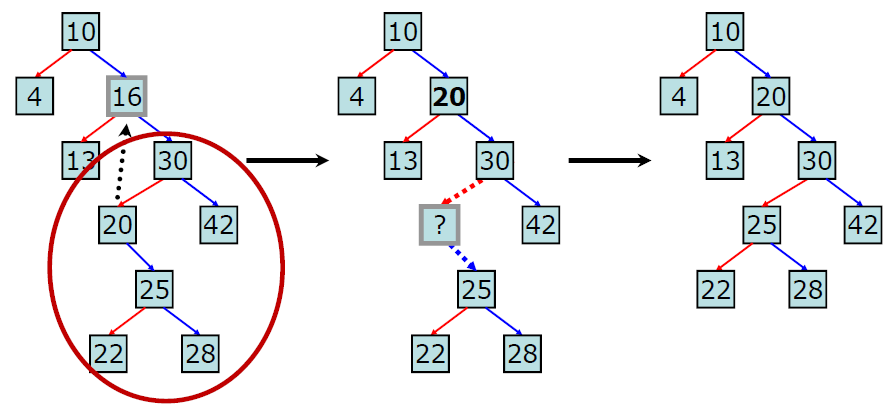
삭제 노드와 가장 가까운 노드를 찾아서 해당 위치에 대체해주면 된다
- 왼쪽 서브트리에서 가장 오른쪽 노드 or 오른쪽 서브트리에서 가장 왼쪽 노드를 삭제노드에 대체
- 가장 가까운 노드의 자식 노드를 부모에 연결