그래프
그래프
그래프는 연결되어 있는 원소 간의 관계를 표현한 자료구조이다.
연결할 객체를 나타내는 정점과 객체를 연결하는 간선의 집합으로 구성된다.
그래프 용어
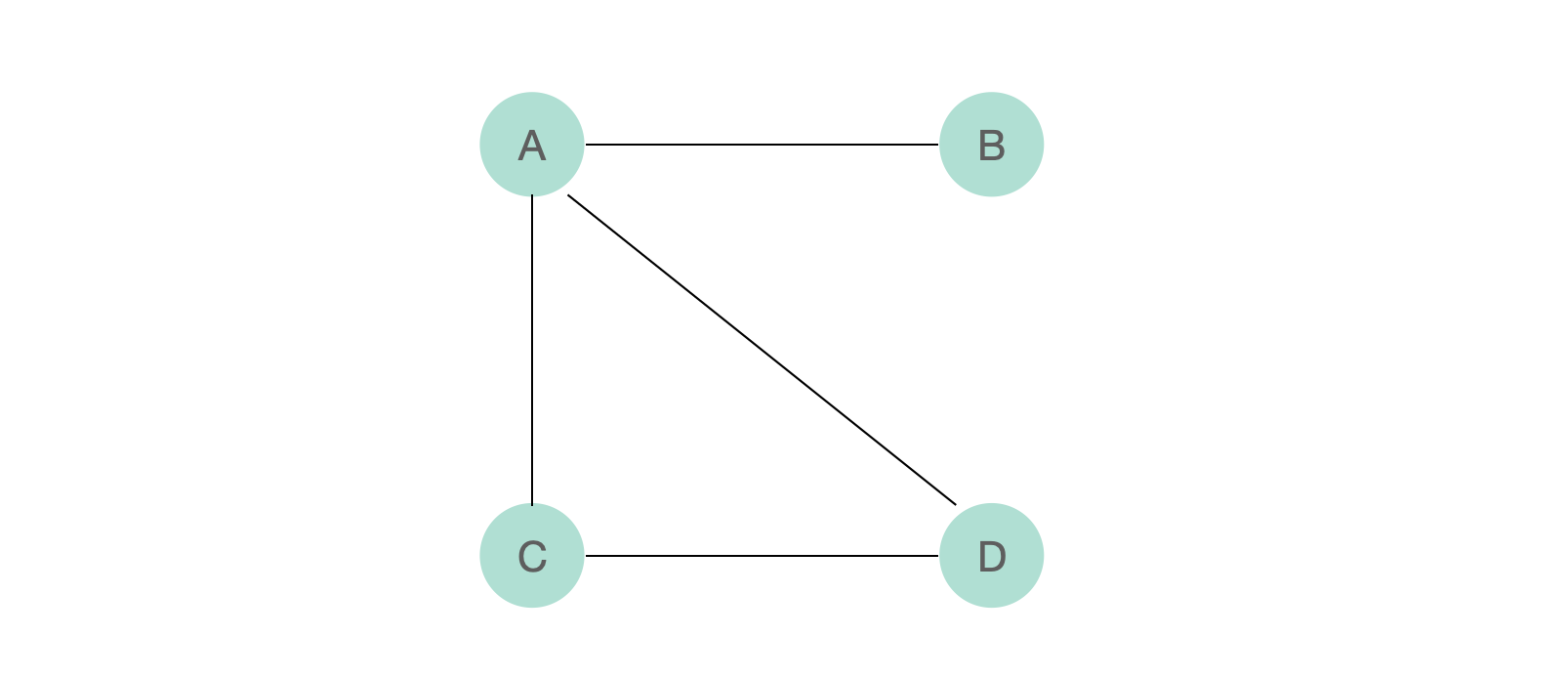
- 정점(vertex) (=node) : 데이터가 저장되는 그래프 기본 원소
- 인접 정점 adjacent vertex : 간선에 의해 직접 연결된 정점( 그림에서 A,C 는 인접정점이다)
- 간선(edge) (=link) : 정점간의 관계를 나타내는 링크
- 경로(path) : 간선을 따라 갈 수 있는 길
- 단순경로(simple path) : 경로 중에서 반복되는 간선이 없는 경로
- 사이클(cycle) : 단순 경로의 시작과 종료지점이 같은 경로
- 단순경로(simple path) : 경로 중에서 반복되는 간선이 없는 경로
- 차수(degree) : 정점에 연결된 간선의 수
- 진출 차수(out-degree) : 외부로 향하는 간선의 수
- 진입 차수(in-degree) : 외부에서 들어오는 간선의 수
- 트리(Tree) : 사이클을 가지지 않는 연결 그래프
그래프 종류
무방향 그래프(undirected graph)
간선에 방향이 표시 되지 않은 그래프
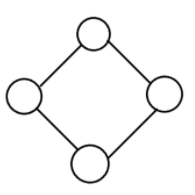
방향 그래프(directed graph)
간선에 방향성이 존재하는 그래프
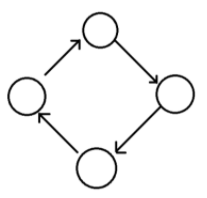
가중치 그래프(weighted graph)
간선에 비용이나 가중치가 할다된 그래프
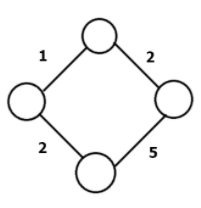
연결 그래프(connected graph)
모든 정점 사이에 경로가 존재하는 그래프 ↔ 비연결 그래프
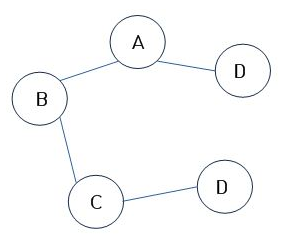
완전 그래프(complete graph)
모든 정점 간에 간선이 존재하는 그래프
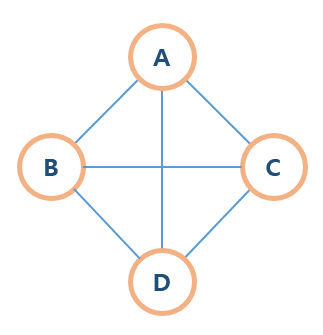
그래프의 구현 방법
크게 2가지 방법이 있다.
인접행렬 Adjacency Matrix
결국 그래프에서 간선은 정점과 정점을 이어준다.
이러한 대전제를 바탕으로 행렬을 이용해서 표현할 수 있다.
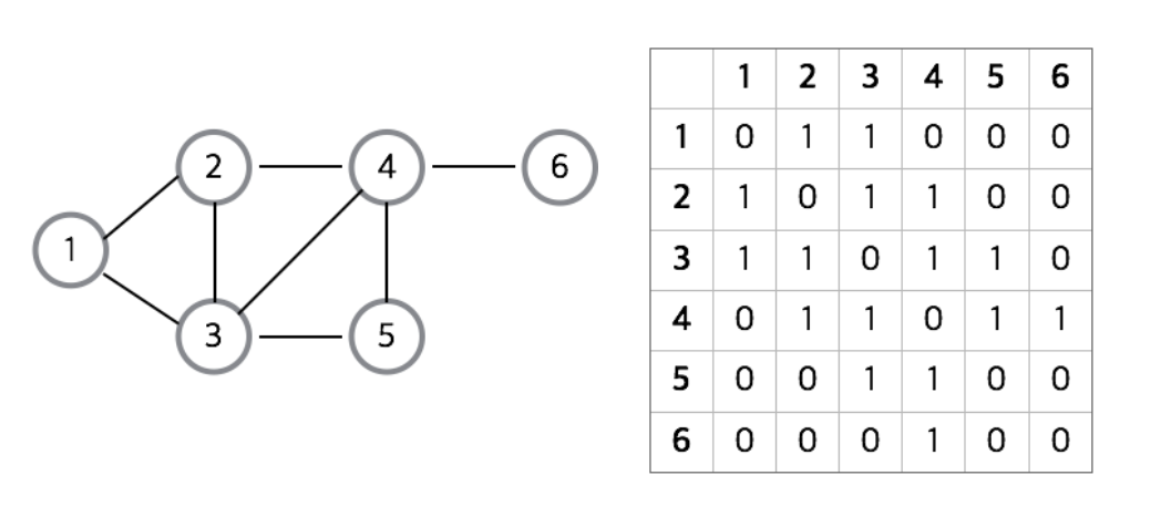
정점의 수가 n일 때 n x n의 행렬을 만들고, 행렬에 정점간의 간서의 정보를 표현한다.
정점 사이에 간선이 존재하면 1, 없으면 0으로 표시한다. 만일 가중치 그래프의 경우 가중치 값을 넣어준다.
무방향 그래프의 경우 대칭 행렬이 되고 방향 그래프의 겨우 비대칭 행렬이 된다.
- 간선의 존재 여부나 가중치를 알고 싶을 때 바로 참조할 수 있다. → O(1)
- 간단하게 구현할 수 있다.
- NxN 의 배열을 사용해서 메모리가 필요이상으로 많이 사용된다.
→ 정점은 많은데 간선이 적은 경우 특히. - 간선에 정보 입력하고, 간선의 수를 알아내는데 O(
)의 시간이 요구된다.
인접 리스트 Adjacency List
체이닝 방법이라고 생각하면 된다.
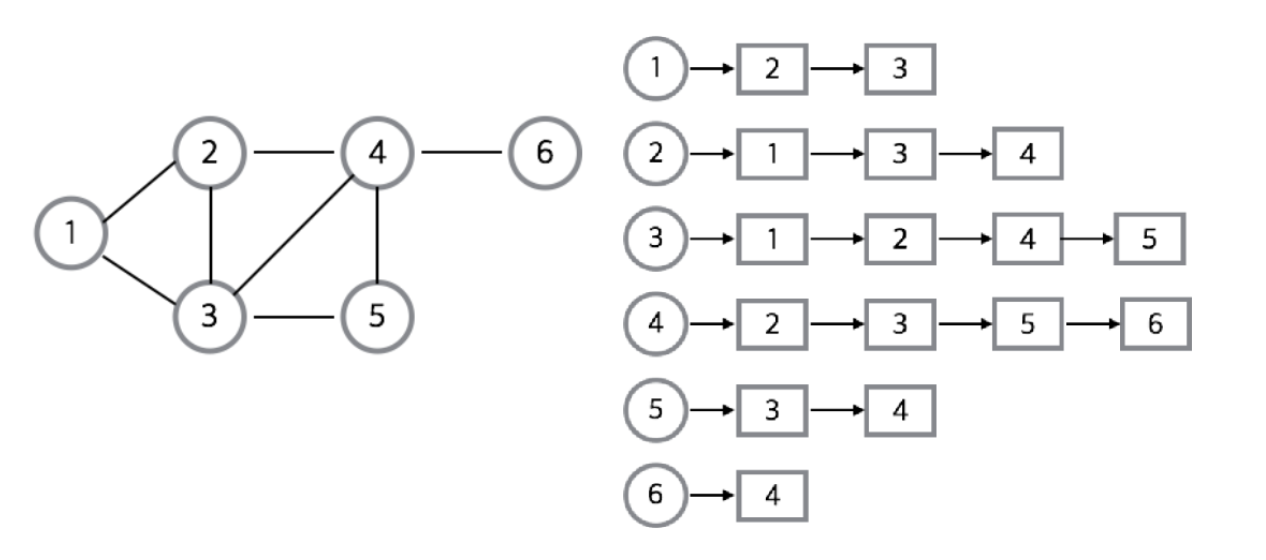
연결리스트를 사용하여 정점에 연결되어 있는 정점들을 리스트로 나타내는 방식이다.
- 필요한 만큼 메모리를 사용해서 낭비가 없다.
- 정점들의 연결정보를 확인할 때는 간선의 갯수만큼 탐색 해야한다. 즉, **정점에 연결된 간선의수가 N일 때 O(
)을 갖는다.