위상정렬

간단하게 말하자면 어떤 일을 하는 순서를 찾는 알고리즘이다.

c92e57cb5c3129c18a6b5de4d45c1149_MD5.jpeg

과목으로 예시를 들 수 있다.
자료구조 → 알고리즘 → 고급 알고리즘 순서로 수업을 들어야 할 경우, 선수과목인 알고리즘을 수강하지 않고 고급 알고리즘을 수강하면 안된다. 이러한 방향성있는 노드에 대한 순서를 찾는 알고리즘이다.

  1. 작업의 우선 순위 결정
  2. 종속 관계 해결
  3. 의존성 분석
위상정렬을 구현하는 방법에는 크게 2가지가 있다.

  1. In-degree 방법(BFS)
  2. DFS를 사용하는 방법

In-degree

진입 차수와 진출 차수

in-degree는 진입차수를 의미한다.
그래서 in-degree방법을 사용하기 위해서 진입 차수와 진출 차수에 대한 이해가 필요하다.

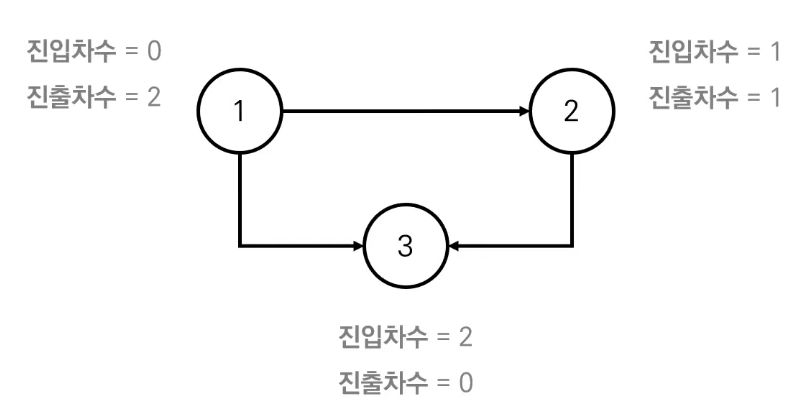
cf7af3144d67f3905f5a955c315ad3c8_MD5.jpeg

동작 과정

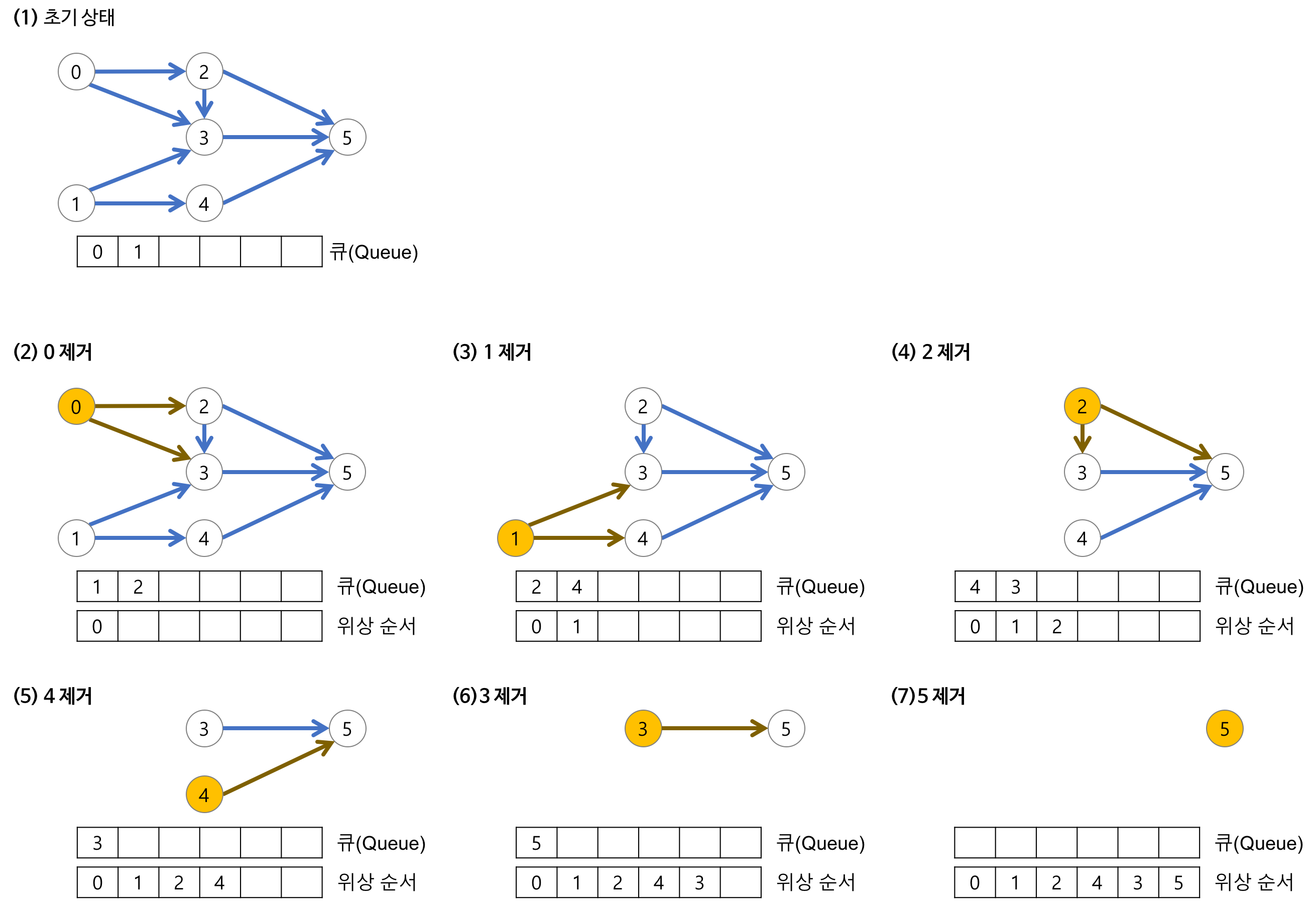
Pasted image 20231013170411.png|출처:https://gmlwjd9405.github.io/2018/08/27/algorithm-topological-sort.html

  1. 모든 노드의 진입차수 계산, 진입차수가 0인 노드가 시작 노드가 됨.
  2. 진입차수가 0인 노드를 큐에 삽입
  3. 큐에서 꺼낸 노드에서 나가는 간선을 그래프에서 제거
  4. 제거된 간선과 연결된 노드들의 진입차수 갱신

2~4번의 과정이 반복되어 모든 노드들이 큐에 삽입되고 제거된다. 제거된 순서가 위상정렬의 결과가 된다.

구현

def topological_sort(graph):
    # 진입차수를 저장할 딕셔너리 생성 및 초기화
    in_degree = defaultdict(int)
    
    # 모든 노드의 진입차수 계산
    for node in graph:
        for neighbor in graph[node]:
            in_degree[neighbor] += 1

    # 진입차수가 0인 노드를 큐에 추가
    queue = deque([node for node in graph if in_degree[node] == 0])
    
    # 위상 정렬 결과를 저장할 리스트 생성
    result = []

    # 큐에서 노드를 제거하면서 위상 정렬 수행
    while queue:
        node = queue.popleft()
        result.append(node)
        
        # 제거한 노드의 이웃 노드들의 진입차수를 감소시키고, 진입차수가 0이 되는 노드를 큐에 추가
        for neighbor in graph[node]:
            in_degree[neighbor] -= 1
            if in_degree[neighbor] == 0:
                queue.append(neighbor)

    # 사이클이 존재하는 경우 위상 정렬이 불가능하므로, 결과 리스트의 길이와 그래프의 노드 수를 비교하여 확인
    if len(result) != len(graph):
        raise ValueError("사이클이 존재하여 위상 정렬이 불가능합니다.")
    
    return result

시간복잡도

정점의 수 V, 간선의 수 E 일 떄

DFS 위상정렬

결국 위상정렬은 모든 노드를 순서대로 탐색하는 방법이기 때문에 그래프를 탐색하는 방법을 살짝 변형한 거다. in-degree도 진입 차수라는 개념만 살짝 사용한 bfs라고 볼 수 있다.
dfs를 사용한 방법으로도 위상정렬을 구현할 수 있다.

동작과정

  1. 모든 정점 순회하면서 방문하지 않은 정점에 대해서 DFS 수행
  2. DFS를 수행하는데 DFS가 끝나면 해당 노드를 결과 리스트 맨 앞에 추가

448997140660c66ef6965ef1d25f43e5_MD5.jpeg

구현

from collections import defaultdict

def topological_sort_dfs(graph):
    # DFS 함수 정의
    def dfs(node, visited, result):
        visited[node] = True
        for neighbor in graph[node]:
            if not visited[neighbor]:
                dfs(neighbor, visited, result)
        # DFS가 끝나면 해당 노드를 결과 리스트의 맨 앞에 추가
        result.insert(0, node)

    # 방문 여부를 저장할 딕셔너리 생성 및 초기화
    visited = defaultdict(bool)
    
    # 위상 정렬 결과를 저장할 리스트 생성
    result = []
    
    # 모든 노드에 대해 DFS 수행
    for node in graph:
        if not visited[node]:
            dfs(node, visited, result)

    return result

개선

뇌피셜로 위와 같은 구현의 문제점으로 2가지가 있다고 생각.

  1. 재귀
    → 반복문으로 구현
  2. list 맨 앞에 추가하면 O(n)의 시간복잡도 발생
    → 맨 뒤에 추가하고 결과를 뒤집자

시간 복잡도

정점의 수가 V이고 간선의 수가 E일 때

references